2項分布をPythonで理解する

Pythonプログラミングイントロダクション(15章)まで読みました。 15章では確率統計を題材に、正規分布や関連する話題として信頼区間について述べられています。

様々な確率統計の題材について、Pythonでの実装とpylabを用いたグラフ表示付きで説明されているので、写経をしていくことで確率統計の知識が深まります。 その中でも確率分布についてみていこうと思います。

様々な確率分布

この章では様々な確率分布を例にPythonでの実装が例示されています。 この章で学ぶ確率分布の一部を列挙してみました。

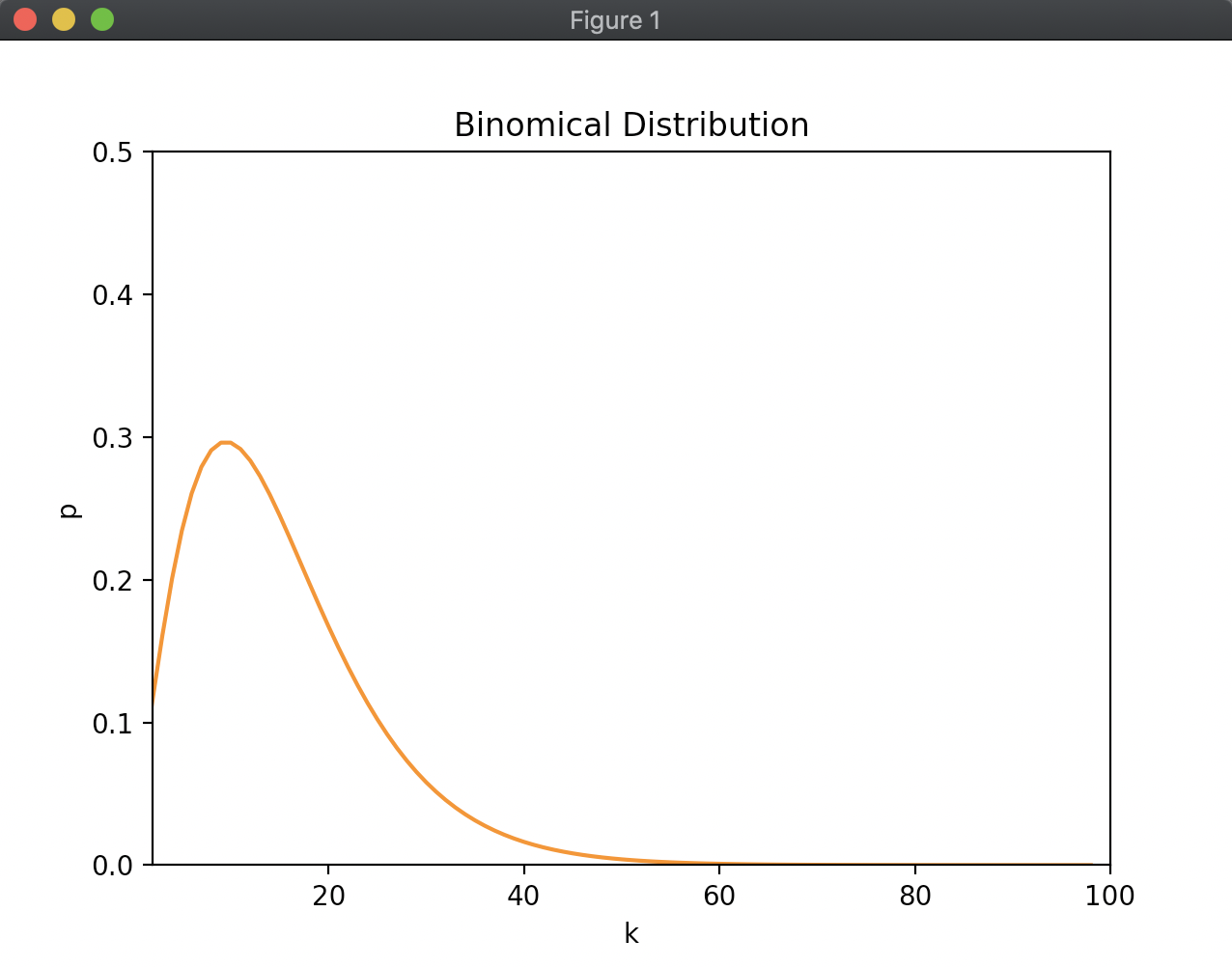
2項分布の練習問題

上記にあげた確率分布の中でも、2項分布については練習問題がついていたのでみていこうと思います。 練習問題は下記になります。

k回の公平なサイコロ投げでちょうど3が2回出る確率を計算する関数を実装せよ。
この関数を用いて、kを2から100まで変化させたときの確率をプロットせよ。

まず、サイコロを投げて3が出る確率は 1/6 になります。 k回サイコロを投げて2回しか3がでず、残りは3以外の数字が出るということになります。 k回サイコロを投げて3が2回出る組み合わせを考える必要があります。

k = 2 のときは

k = 3 のときは、1,2回目が3の時、1,3回目が3の時、2,3回目が3の時の3通りの確率を足し合わせます。

このような2項分布と呼ばれる確率分布の式は以下で表されます。

Pythonでの実装は下記のようになります。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import math
import pylab

def binomical_distribution(k, p, t):
    c = math.factorial(k) / (math.factorial(t) * math.factorial(k - t))
    return c * p**t * (1 - p)**(k - t)


def show_plot(p, t):
    x, y = [], []
    for k in range(t, 101):
	x.append(k)
	y.append(binomical_distribution(k, p, t))

    pylab.plot(x)
    pylab.plot(y)
    pylab.ylim(0, 0.5)
    pylab.xlim(2, 100)
    pylab.xlabel('k')
    pylab.ylabel('p')
    pylab.title('Binomical Distribution')
    pylab.show()

show_plot(1 / 6, 2)

まとめ

2項分布の指練習について、実際にPythonで実装してみました。 この章で学んだ信頼区間についてはこの後でも深掘りされていくようなので楽しみです。