Gside

2020-02-16 in CS, 統計学, Python

仮説検定結果より導いたp値を検証する

Pythonプログラミングイントロダクション(19章) まで読みました。 19章では統計的仮説検定についてです。

自転車競技の記録を伸ばす薬であるPED-XとPED-Yのどちらが優れているか無作為試験を行った結果から、得られた平均タイムについて検討していきます。本当に平均タイムに有意な差があるのか、偶然発生した差なのかを検定をする方法が説明されています。

フィッシャーの統計的仮説検定

本書で述べられているフィッシャーの統計的仮説検定の手順は下記になります。この手順により観測結果が偶然起こったのか確率を評価していきます。

1. 帰無仮説(null hypothesis)と対立仮説(alternative hypothesis)を立てる.
2. 評価する標本についての統計的仮定を理解する.
3. 適切な検定統計量(test statistic)を計算する.
4. 帰無仮説における検定統計量の確率を得る.
5. その確率が、帰無仮説が偽であると推測できるほどに十分小さいかどうか,すなわち,帰無仮説を棄却(reject)するかどうかを決定する.

1. 帰無仮説(null hypothesis)と対立仮説(alternative hypothesis)を立てる.

PED-XとPED-Yの平均値を例にとった場合、下記のようになります。

帰無仮説：PED-XとPED-Yの平均の差が0

対立仮説：PED-XとPED-Yの平均の差が0でない

2. 評価する標本についての統計的仮定を理解する.

PED-XとPED-Y使用者のフィニッシュタイムは正規分布となり、標本は無限母集団から抽出した物でした。

3. 適切な検定統計量(test statistic)を計算する.

t値を計算します。t値とは二つの平均の誤差が標準誤差で見て0からどれくらい差があるかを表した値です。本書では-2.13165598142となりました。

標準誤差は17章で出てきたものです。

\( \sigma_{a}^{2} : 母集団の分散 \\\ \sigma_{a} : 母集団の標準偏差 \\\ n : 標本サイズ \)

\[ SE = \frac{\sigma}{\sqrt{n}} \]

4. 帰無仮説における検定統計量の確率を得る.

p値を計算します。p値とは帰無仮説が成立する前提で、統計量が観測された値以上の極端な値が得られる確率のことです。つまり、PED-XとPED-Yがの平均の差が0であったときに差が現れるような極端な値が得られる確率のことになります。本書では0.0343720799815、つまり3.4%程になりました。

5. その確率が、帰無仮説が偽であると推測できるほどに十分小さいかどうか,すなわち,帰無仮説を棄却(reject)するかどうかを決定する.

本書ではp値が3.4%となり、PED-Xの方が優れていそうと言う結論になりかけますが、この後p値が信用ならないと言う話につながっていきます。

p値を何度も計算してみる

本書を読み進めていくと、この例はプログラムにより作り出されたデータであると言うたねあかしがされます。平均値119.5、標準偏差5.0の分布と平均値120.0、標準偏差が4.0の分布からランダムにサンプリングした値が使われていました。 random.gauss関数でデータを作っています。

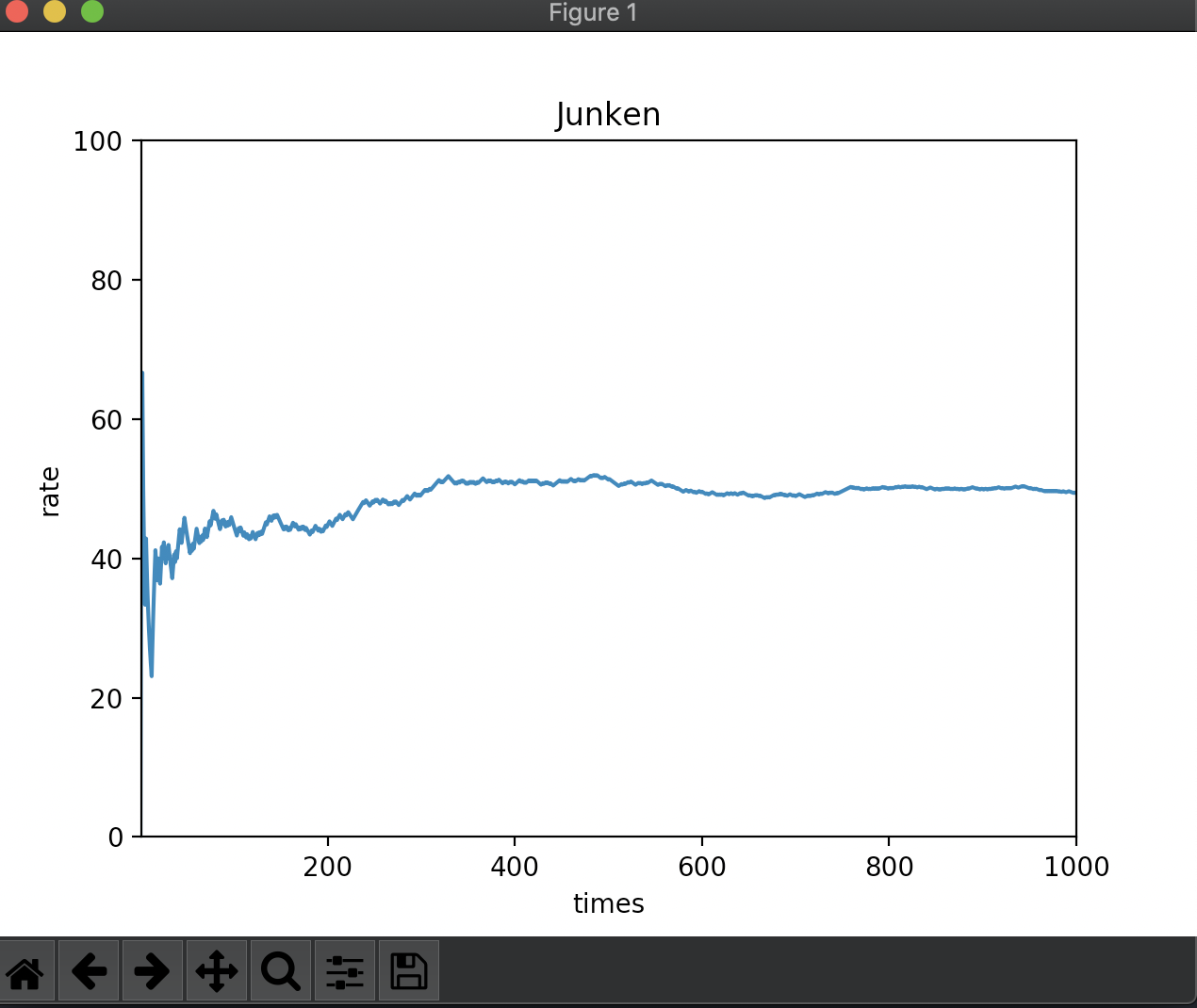
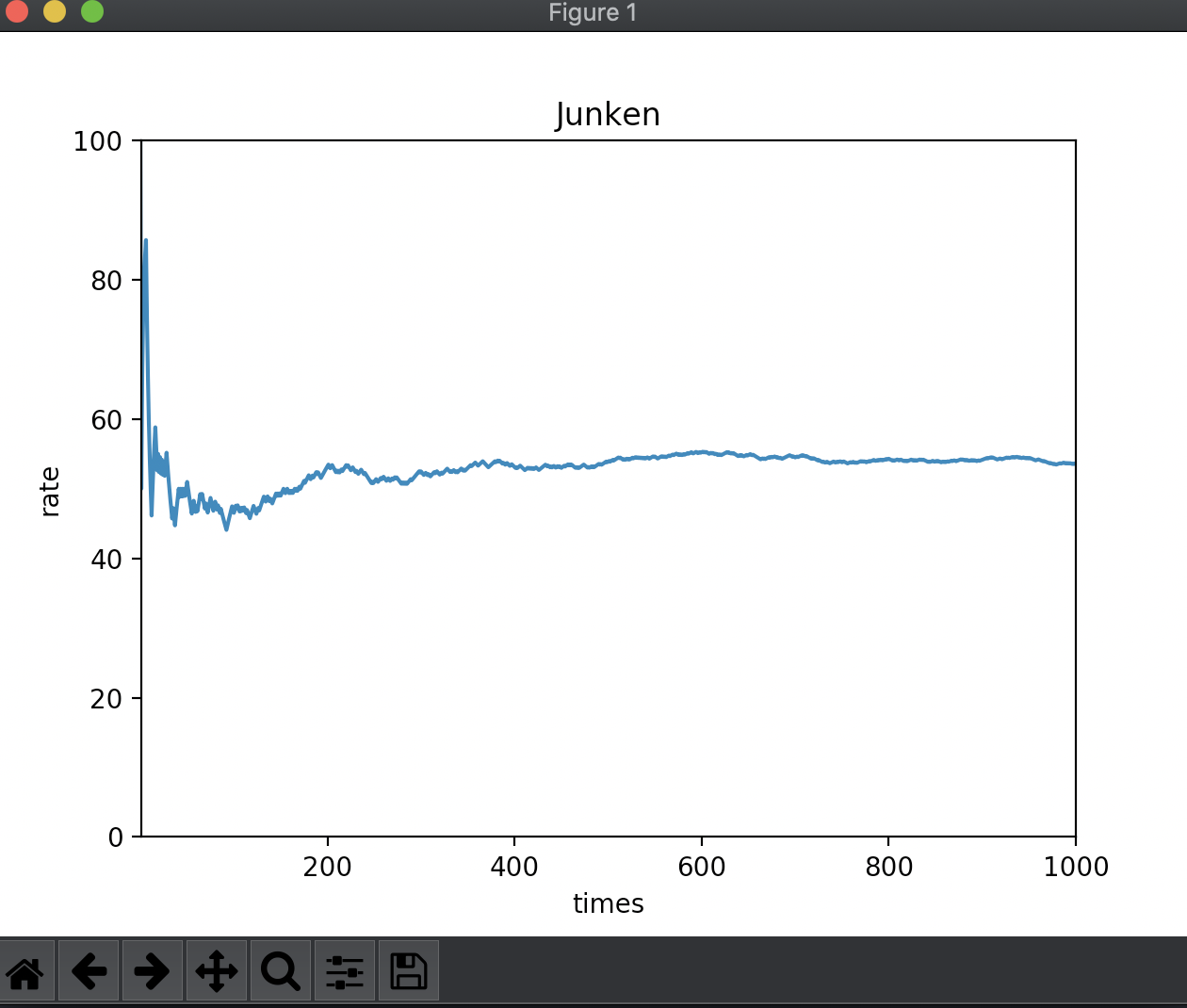
実際に何度か下記のようなプログラムを流してみると、p値の値は乱高下します。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import random
from scipy import stats


def get_t_value():
    treatmenDist = (119.5, 5.0)
    controlDist = (120, 4.0)
    sampleSize = 1000

    treatmentTimes, controlTimes = [], []

    for s in range(sampleSize):
        treatmentTimes.append(random.gauss(treatmenDist[0], treatmenDist[1]))
        controlTimes.append(random.gauss(controlDist[0], controlDist[1]))

    controleMeans = sum(controlTimes) / len(controlTimes)
    treatMeans = sum(treatmentTimes) / len(treatmentTimes)

    twoSampleTest = stats.ttest_ind(treatmentTimes, controlTimes, equal_var=False)
    print('Treatmeant mean - control mean = ',
          treatMeans - controleMeans, ' minutes')
    print('The t-statistic from two-sample test is ', twoSampleTest[0])
    print('The p-value from two-sample test is ', twoSampleTest[1])


for i in range(10):
    twoSampleTest = get_t_value()

結果は下記のようになります。p値が1%台の時もあれば60%台の時もあります。

Treatmeant mean - control mean =  -0.6843325129559474  minutes
The t-statistic from two-sample test is  -1.0716961219246917
The p-value from two-sample test is  0.285226164284344
Treatmeant mean - control mean =  -0.39645994742086543  minutes
The t-statistic from two-sample test is  -0.6751950331252392
The p-value from two-sample test is  0.5004085432884583
Treatmeant mean - control mean =  0.25269386654427706  minutes
The t-statistic from two-sample test is  0.3950053957541872
The p-value from two-sample test is  0.6932658871131978
Treatmeant mean - control mean =  0.50100925426743  minutes
The t-statistic from two-sample test is  0.7660580410192988
The p-value from two-sample test is  0.4445624847162438
Treatmeant mean - control mean =  -0.9383152222142996  minutes
The t-statistic from two-sample test is  -1.3925614858916715
The p-value from two-sample test is  0.16555904568337207
Treatmeant mean - control mean =  -0.4504161747373985  minutes
The t-statistic from two-sample test is  -0.7134525526996994
The p-value from two-sample test is  0.4764536661236095
Treatmeant mean - control mean =  -0.517887936147531  minutes
The t-statistic from two-sample test is  -0.818800036206608
The p-value from two-sample test is  0.41390883875821693
Treatmeant mean - control mean =  -0.7535810558372305  minutes
The t-statistic from two-sample test is  -1.2462075073793941
The p-value from two-sample test is  0.21417712992121332
Treatmeant mean - control mean =  -1.5033637291589912  minutes
The t-statistic from two-sample test is  -2.347673847276862
The p-value from two-sample test is  0.019992408614120653
Treatmeant mean - control mean =  -0.3150896341041829  minutes
The t-statistic from two-sample test is  -0.5046312441817462
The p-value from two-sample test is  0.6144229896604907

と言うことで、200程度のサンプリング数だとp値がこれだけ上下することが示されました。

まとめ

仮説検定についての流れを追ってみました。取り上げた流れは2標本の両側検定と言うものです。本書では他にも片側検定と1標本検定についての話題も取り扱っています。

本書ではp値が低いのは帰無仮説が実際に低いかもしれないし、母集団の代表的な例でない場合もあると言われています。そして、このp値の問題を解決する考え方として20章のベイズ統計に続いていくわけです。

2020-02-10 in CS, 統計学, Python

中心極限定理をアニメレーティングデータで検証する

Pythonプログラミングイントロダクション(17章) まで読みました。 17章では中心極限定理について説明されています。

この章の目標の一つは「一つの標本から標本平均の信頼度を出す」ことにあります。そのための道具として中心極限定理を利用します。

中心極限定理

中心極限定理についての引用は下記になります。

- 同じ母集団から抽出された標本サイズが十分に大きいと、標本の平均(標本平均)はおおよそ正規分布に従う
- この正規分布の平均は母集団の平均に非常に近い。
- 標本平均の分散は母集団の分散を標本サイズで割ったものに非常に近い

中心極限定理により標本平均は正規分布に従います。

また、標本平均の分散は母集団の分散を標本サイズで割ったものに非常に近いという事は、標本平均の標準偏差は母集団の標準偏差を標本サイズの平方根で割ったものに非常に近いということになります。これを式にすると、標本平均の標準偏差を求める式は下記のようになります。

\( \sigma_{a}^{2} : 母集団の分散 \\\ \sigma_{a} : 母集団の標準偏差 \\\ \sigma_{s}^{2} : 標本平均の分散 \\\ \sigma_{s} : 標本平均の標準偏差 \\\ n : 標本サイズ \)

\[ \sigma_{s}^{2} = \frac{\sigma_{a}^{2}}{n} \] \[ \sigma_{s} = \frac{\sigma_{a}}{\sqrt{n}} \]

母集団の標準偏差を標本サイズの平方根で割ったものは標準誤差とも言われます。そしてこのとき必要な母集団の標準偏差は、ある一定数の標本サイズがあれば標本の標準偏差を用いて良いとされているそうです。

まとめると、下記の手順で中心極限定理が正しいかを見ていきます。

標本の値から標準偏差を求め、母集団の標準偏差とする。
標本平均の標準偏差を求める。
この標準偏差から95%信頼区間を導きます。
実際の母集団の平均値と標本平均の誤差を求める

アニメのレーテイングデータで検証する

kaggleのサイトでアニメのレーティングに関するデータを利用させていただきました。本書と同様の手順でこのデータから標本サイズ200のデータを元に信頼区間を導き、実際の母集団から求めた平均との絶対誤差を元に信頼区間の値が妥当を見ていきます。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import random
import pylab
import csv

def variance(X):
    """分散"""
    mean = sum(X)/len(X)
    tot = 0.0
    for x in X:
        tot += (x - mean)**2
    return tot/len(X)


def stdDev(X):
    """標準偏差(分散の平方根)"""
    return variance(X)**0.5

def read_anime_score(path):
    """データを読み込みスコアのリストを返す"""
    scores = []
    with open(path, newline='') as f:
        reader = csv.reader(f)
        # skip header
        next(reader)
        for row in reader:
            scores.append(float(row[15]))

    return scores

data = read_anime_score('./anime_cleaned.csv')

# 母平均
popMean = sum(data) / len(data)
# 標本サイズ
sampleSize = 200
numBad = 0
for t in range(10000):
    sample = random.sample(data, sampleSize)
    # 標本平均
    sampleMean = sum(sample) / sampleSize
    # 標準誤差
    se = stdDev(sample) / sampleSize**0.5

    # 母平均と標本平均の誤差から信頼区間外のデータ数を求める
    if abs(popMean - sampleMean) > 1.96 * se:
        numBad += 1
print('Fraction outside 95% confidence interval =', numBad / 10000)

: Fraction outside 95% confidence interval = 0.05

概ね5%程度の結果が求められます。中心極限定理で定義されている通り、標本サイズが十分大きいと標本平均が正規分布に従い、母集団の平均に非常に近いと言えそうです。

まとめ

本章は話の流れがわかりにくかったので最初は何を言っているのか正直わかりませんでしたが、まとめてみると最終的に標本平均から信頼区間を求めたいのだとわかりました。

母集団の標準偏差が標本の標準偏差で代用できる点は気持ちの悪いところですが、本書でも下記のように説明されています。

多くの統計学者が言うには、母集団の分布がおおよそ正規分布であれば標本サイズが30から40で十分に大きい。
標本サイズが小さい場合にはt分布と呼ばれるものを使って区間計算したほうが良い。

t分布はこの後出てくるようなので一旦読み進めていくとします。

2020-01-04 in CS, 統計学, Python

ジャンケンをモンテカルロ・シミュレーションしてみる

Pythonプログラミングイントロダクション(16章) まで読みました。 16章ではモンテカルロ・シミュレーションについての説明になります。

モンテカルロ・シミュレーションって大そうな名前がついていますが、この章までにやってきたランダムネスを利用したシミュレーションのことをモンテカルロ・シミュレーションといいます。この章でもサイコロゲームを題材にランダムネスを利用したモンテカルロシミュレーションの実装がいくつか例示されています。

ランダムネスで円周率を求めるプログラミングなんかは痺れました。

ジャンケンのシミュレーション

ここではジャンケンのモンテカルロ・シミュレーションをPythonで実装して理解を深めていきたいと思います。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import pylab
import random


def janken():
    JANKEN_PATTERN = ['G', 'C', 'P']
    while True:
        a_t = random.choice(JANKEN_PATTERN)
        b_t = random.choice(JANKEN_PATTERN)
        if a_t != b_t:
            break
    return janken_judge(a_t, b_t)


def janken_kai():
    JANKEN_WIN_PATTERN = ['G', 'G', 'C', 'P']
    JANKEN_LOSE_PATTERN = ['G', 'C', 'C', 'P']
    while True:
        a_t = random.choice(JANKEN_WIN_PATTERN)
        b_t = random.choice(JANKEN_LOSE_PATTERN)
        if a_t != b_t:
            break
    return janken_judge(a_t, b_t)


def janken_judge(a_t, b_t):
    """ a_tとb_tは違う値の想定。
    aが勝っていたらTrue, 負けていたらFalseを返す """

    win_pattern = [('G', 'C'), ('C', 'P'), ('P', 'G')]
    return (a_t, b_t) in win_pattern


def show_plot(trials, target):
    a_rate = []
    a_win = 0
    for k in range(1, trials + 1):
        if target():
            a_win += 1

        a_rate.append(a_win / k * 100)
    pylab.plot(a_rate)
    pylab.ylim(0, 100)
    pylab.xlim(1, trials)
    pylab.xlabel('times')
    pylab.ylabel('rate')
    pylab.title('Junken')
    pylab.show()


def get_stdDev(trials):
    a_rate = []
    for i in range(0, 100):
        a_win = 0
        for k in range(0, trials):
            if janken():
                a_win += 1
        a_rate.append(a_win / k * 100)
    return stdDev(a_rate)


def variance(X):
    """分散"""
    mean = sum(X)/len(X)
    tot = 0.0
    for x in X:
        tot += (x - mean)**2
    return tot/len(X)


def stdDev(X):
    """標準偏差(分散の平方根)"""
    return variance(X)**0.5


show_plot(1000, janken)
show_plot(1000, janken_kai)
print('10 trials stdDev: ', get_stdDev(10))
print('100 trials stdDev: ', get_stdDev(100))
print('1000 trials stdDev: ', get_stdDev(1000))

janken関数では、a,bそれぞれのグー(G)、チョキ(C)、パー(P)の中からランダムに選択した上で勝ち負けを判定しています。あいこの場合はもう一度ランダムに選択しなおします。

完全にランダムにグー、チョキ、パーを選ぶ場合は試行回数が増えるについれて勝率は5割に近づいていきます。 15章で学んだ大数の法則の通りですね。

人間がジャンケンをする場合は完全にランダムとはいかず、グー、チョキ、パーのどれかに選択が偏ることがあるでしょう。ランダムではありますが、aさんがグーを出しがち、bさんがチョキを出しがちな場合はaさんの勝率が上がっていきます。そんなjanken_kaiを作ってみました。この場合はaさんの勝率が5割より上回っていますね。

続いて標準偏差を出してみました。試行回数を増やすにつれ、標準偏差が減っていきます。

: 10 trials stdDev:  17.91612832955234
: 100 trials stdDev:  5.337158102067871
: 1000 trials stdDev:  1.6880153857382443

まとめ

これまで学んだ統計の知識を織り交ぜつつ、ジャンケンを題材にモンテカルロ・シミュレーションをやってみました。ここ何章かは思ったより統計学の内容が多いことに若干戸惑いもありましたが、内容も楽しいですしトレンド的にも良い題材なのかと思います。 Pythonを学ぶついでに統計学も学べるお得な一冊だと思います。

2020-01-01 in CS, 統計学, Python

2項分布をPythonで理解する

Pythonプログラミングイントロダクション(15章)まで読みました。 15章では確率統計を題材に、正規分布や関連する話題として信頼区間について述べられています。

様々な確率統計の題材について、Pythonでの実装とpylabを用いたグラフ表示付きで説明されているので、写経をしていくことで確率統計の知識が深まります。その中でも確率分布についてみていこうと思います。

様々な確率分布

この章では様々な確率分布を例にPythonでの実装が例示されています。この章で学ぶ確率分布の一部を列挙してみました。

名称	内容
一様分布	サイコロの目の出る確率のように全ての事象の起こる確率が等しい確率分布
2項分布	成功か失敗のように2つの値しか取らないような場合の確率分布
多項分布	2項分布と異なり、3つ以上の値を取るような場合の確率分布
指数分布	人体の薬物濃度のように指数関数的に濃度が減少していくような場合の確率分布

2項分布の練習問題

上記にあげた確率分布の中でも、2項分布については練習問題がついていたのでみていこうと思います。練習問題は下記になります。

k回の公平なサイコロ投げでちょうど3が2回出る確率を計算する関数を実装せよ。
この関数を用いて、kを2から100まで変化させたときの確率をプロットせよ。

まず、サイコロを投げて3が出る確率は 1/6 になります。 k回サイコロを投げて2回しか3がでず、残りは3以外の数字が出るということになります。 k回サイコロを投げて3が2回出る組み合わせを考える必要があります。

k = 2 のときは

\[ \frac{1}{6} * \frac{1}{6} \]

k = 3 のときは、1,2回目が3の時、1,3回目が3の時、2,3回目が3の時の3通りの確率を足し合わせます。

\[ \frac{1}{6} * \frac{1}{6} * \frac{5}{6} + \frac{1}{6} * \frac{5}{6} * \frac{1}{6} + \frac{5}{6} * \frac{1}{6} * \frac{1}{6}\]

このような2項分布と呼ばれる確率分布の式は以下で表されます。

\[ {}_k \mathrm{ C }_t P^t(1 - P)^{k - t} = \frac { k! } { t!(k - t)! } P^t(1 - P)^{k - t} \]　

Pythonでの実装は下記のようになります。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import math
import pylab

def binomical_distribution(k, p, t):
    c = math.factorial(k) / (math.factorial(t) * math.factorial(k - t))
    return c * p**t * (1 - p)**(k - t)


def show_plot(p, t):
    x, y = [], []
    for k in range(t, 101):
	x.append(k)
	y.append(binomical_distribution(k, p, t))

    pylab.plot(x)
    pylab.plot(y)
    pylab.ylim(0, 0.5)
    pylab.xlim(2, 100)
    pylab.xlabel('k')
    pylab.ylabel('p')
    pylab.title('Binomical Distribution')
    pylab.show()

show_plot(1 / 6, 2)

まとめ

2項分布の指練習について、実際にPythonで実装してみました。この章で学んだ信頼区間についてはこの後でも深掘りされていくようなので楽しみです。

2019-12-24 in Python, 統計学, Book

「統計学が最強の学問である(数学編)」で機械学習の入り口に連れて行ってもらおう

「統計学が最強の学問である(数学編)」を読み終わりました。機械学習を学ぶための数学の知識を叩き込んで、機械学習の入り口まで連れて行くぞという著者の意志を強く感じる本でした。

記号論理学から始まって、連立方程式、線形代数、微分積分まで、幅広い知識の中から機械学習に必要なエッセンスを詰め込みながら、機械学習・ディープラーニングの入り口まで連れて行ってくれる一冊になっています。

内容

この本の流れを簡単にまとめると下記のようになります。

簡単な確率、記号論理学、集合から最終的には迷惑メールフィルタでも用いられていたナイーブベイズ
1次、2次の関数を学び、ちょうど良い数を求めるための平方完成
二項定理から二項分布、対数、ネイピア数について
たくさんの数を効率的に表記するためにΣ、ベクトル、行列
ちょうど良いところを探すための微分、確率密度関数を理解するための積分
線形代数と微積分を同時に使うことで機械学習、ディープラーニングの入り口へ！

やはりクライマックスはこれまでの知識を積み上げて機械学習の入り口が見えてくる6章です。特に行列、偏微分のありがたみがわかった最小二乗法の解法はしびれました。

行列、偏微分を用いた最小二乗法とnumpy

2章では訪問回数と契約件数のデータを元に比例関係の式を最小二乗法で2章で学んだ最小二乗法は平方完成により答えをめました。 6章ではこれまで学んできた知識、つまり微分、行列を使った解法を解説してくれています。

下記が2章の例示されていたデータになります。

訪問回数(単位:100回)	契約件数(単位:1件)
1	10
2	40
3	82

上記の表で表されるモデルが訪問回数をx, 契約件数をyとした場合に直線で表されるとします。この場合にモデルを表す式は下記のようになります。

\[ y = a + bx + \varepsilon \]

εが誤差でこの誤差を最小にするa, bを求めます。データは3つありますので、それぞれx, yに代入すると3つの式が出てくるわけですが、これを行列で表現すると3つの式ではなく一つの行列式で表すことができます。

\[ y = X\beta + \varepsilon \]

X, y, β,εはそれぞれ下記のような行列になります。

\[X = \begin{pmatrix} 1 & x_1 \ 1 & x_2 \ . & . \ . & . \ 1 & x_n \end{pmatrix} , y = \begin{pmatrix} y_1 \ y_2 \ . \ . \ y_n \end{pmatrix} , \beta = \begin{pmatrix} a \ b \end{pmatrix} , \varepsilon = \begin{pmatrix} \varepsilon_1 \ \varepsilon_2 \ . \ . \ \varepsilon_n \end{pmatrix} \]

εの二乗和が最小になるようなa, とbを求めるのが最小二乗法です。行列の場合、誤差の二乗の和を求める方法としてはεの転置行列とεの内積で表現することができます。

\[ \varepsilon^{ \mathrm { T } }\varepsilon \]

この二乗和が最小になる時のa,bを求めるためにβで偏微分してやります。

\[ \frac{ \partial \varepsilon^{ \mathrm { T } }\varepsilon } { \partial \beta } \]

ここからは、この章にたどり着くまでに得た行列や偏微分の知識を駆使して進めて行くのですが、詳しい解法は是非本書で確認してみてください。結果として下記の式が得られます。

\[ \beta = (X^{ \mathrm { T } }X)^{-1}X^{ \mathrm { T } }y \]

\[ (X^{ \mathrm { T } }X)\beta = X^{ \mathrm { T } }y \]

この式に今回の例を代入すると、下記のようになります。

\[ \begin{pmatrix} 1 & 1 \ 1 & 2 \ 1 & 3 \end{pmatrix}^{ \mathrm { T } } \begin{pmatrix} 1 & 1 \ 1 & 2 \ 1 & 3 \end{pmatrix} \begin{pmatrix} a \ b \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 \ 1 & 2 & 3 \end{pmatrix} \begin{pmatrix} 10 \ 40 \ 82 \end{pmatrix} \]

ここまでくるとPythonで機械学習をやる上で定番のnumpyを使い、逆行列を用いて傾きと切片を求めることができます。この本で学んだ数学の知識が、自分がこれまで学んできた機械学習の定番、numpyと出会った瞬間でした。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
import numpy

x = numpy.array([[1, 1], [1, 2], [1, 3]])
y = numpy.array([10, 40, 82])

left = numpy.dot(x.T , x)
right = numpy.dot(x.T,  y)
inv_left = numpy.linalg.inv(left)
beta = numpy.dot(inv_left, right)
print(beta)

結果は下記のようになります。

1
[-28.  36.]

データ(今回の場合x, y)が増えていっても、この式に当てはめれば容易に最小二乗法を用いたモデルを導くことができます。

まとめ

自分自身はこの本を読む前に機械学習の本を読み始めてしまっていましたが、これから学習する方には是非ともお勧めしたい一冊です。この本で得た知識を携えて、なんとなく通り過ぎているこれまでの知識をもう一度ブラッシュアップしたいと思います。