Blogs

    in  CS, Algorithm, Python

    重み付き有向グラフの探索を優先順位付きキューで実装してみる

    Pythonプログラミングイントロダクション12章まで読みました。 12章は最適化問題についてです。 空き巣が最適な盗みをはたらくためにはどのようなアルゴリズムで物を選んで盗んでいけば良いかを考えるナップザック問題や、 島をつなぐ橋を丁度一度ずつ渡るような散歩が可能か、オイラーによって定式化されたケーニヒスベルクの橋の問題などのグラフ最適化問題が題材になっています。

    最短路問題としては深さ優先探索と幅優先探索が取り上げて、実装について丁寧に説明してくれています。 グラフ最適化問題の仕上げとして、章の最後に重み付き有向グラフの探索アルゴリズムについての練習問題があります。 この練習問題を元に重み付き有向グラフの探索問題を考えていきました。

    探索アルゴリズム

    練習問題をみていく前に、12章で紹介されている探索アルゴリズムについて軽くみていきます。

    幅優先探索 (breadth first search: BFS)

    まずは探索をスタートするノードに接続する全ての子ノードを探索します。 探索対象がなければ、それぞれの子ノードについて、さらにその子ノードを探索していきます。 まずは同じレベルの子ノードを全て探索してから、次の深さの子ノードを探索していきます。

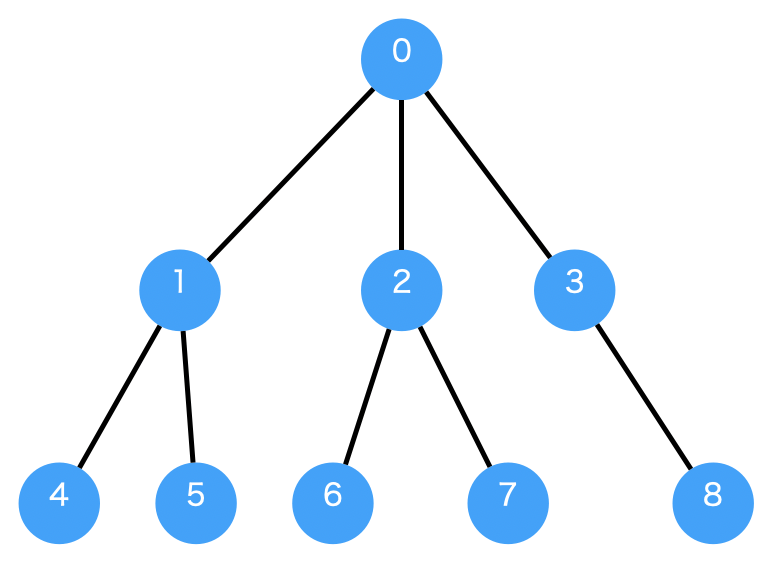
    深さ優先探索 (depth-first search: DFS)

    探索した子ノードにさらに子ノードがあった場合は、その子ノードを優先して探索していきます。 とにかく子ノードが見つかったら真っ先にそちらを探索していく形です。

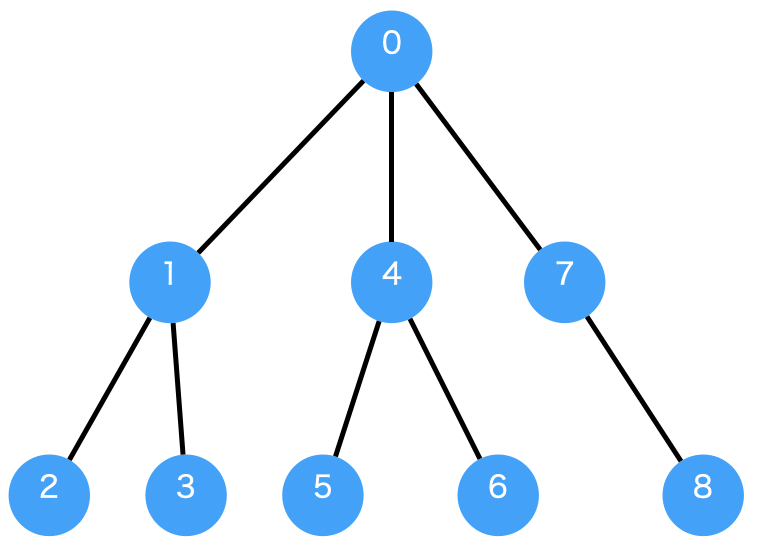
    重み付き有向グラフと幅優先探索

    そして本章の最後には下記の問題が提示されています。

    重み付き有向グラフを考えよう.
幅優先探索アルゴリズムによって最初に見つけられたパスは,
枝の重みの合計が最小であることを保証されているか？

    下記の図は重み付きの有向グラフの例です。ノードをつなぐ枝に重みが付いています。この重みを足した数字が幅優先探索で最小になるかというのが練習問題の問いになります。

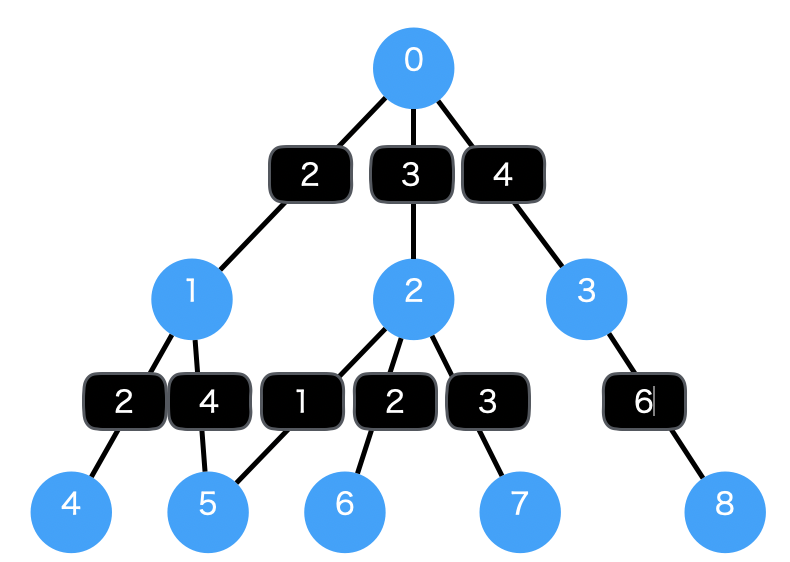
    この例で0からスタートして5を探索する幅優先探索を実施すると0 -> 1 -> 5 (重み6) が導き出されてしまいます。欲しい答えは 0 -> 2 -> 5 (重み4) ですから枝の重みが最小であることは保証されていませんね。 さて、どうすれば良いかというと、優先順位付きキューを用います。この場合、合計した重みが少ないパスを優先的に探索します。

    下記は本書のプログラムを一部拝借しつつ、重みを扱えるようにしました。そして重みが一番少ないパスを探索するUCSメソッドを優先順位付きキューを用いて実装しています。 ちょっと長いですが全部載せておきます。

      1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

    class Node(object):
    def __init__(self, name):
        self.name = name

    def getName(self):
        return self.name

    def __str__(self):
        return self.name

    def __lt__(self, i):
        return None


class WeightedEdge(object):
    """重み付きの枝を表すクラス"""

    def __init__(self, src, dest, weight):
        self.src = src
        self.dest = dest
        self.weight = weight

    def getSource(self):
        return self.src

    def getDestination(self):
        return self.dest

    def getWeight(self):
        return self.weight

    def __str__(self):
        return self.src.getName() + '->(' + str(self.weight) + ')' + self.dest.getName()


class Digraph(object):
    """有向グラフを表すクラス"""

    def __init__(self):
        self.nodes = []
        self.edges = {}

    def addNode(self, node):
        if node in self.nodes:
            raise ValueError('Duplicate node')
        else:
            self.nodes.append(node)
            self.edges[node] = []

    def addEdge(self, edge):
        src = edge.getSource()
        dest = edge.getDestination()
        weight = edge.getWeight()
        if not (src in self.nodes and dest in self.nodes):
            raise ValueError('Node not a graph')

        self.edges[src].append((weight, dest))

    def childrenOf(self, node):
        return self.edges[node]

    def __str__(self):
        result = ''
        for src in self.nodes:
            for dest in self.edges[src]:
                result = result + src.getName() + '->' + dest.getName() + '\n'
        return result[:-1]


def printPath(path):
    """パスを表示するメソッド"""
    result = ''
    for i in range(len(path)):
        result = result + str(path[i])
        if i != len(path) - 1:
            result = result + '->'
    return result


def UCS(graph, start, end):
    """重み付き有向グラフを探索するメソッド"""

    initPath = [start]
    pathQueue = []

    from heapq import heappush, heappop
    heappush(pathQueue, (0, initPath))

    while len(pathQueue) != 0:
        (weight, tmpPath) = heappop(pathQueue)

        print('Current UCS path:', printPath(tmpPath), ' weight:', weight)
        lastNode = tmpPath[-1]

        if lastNode == end:
            return tmpPath
        for (next_weight, nextNode) in graph.childrenOf(lastNode):
            if nextNode not in tmpPath:
                newPath = tmpPath + [nextNode]
                heappush(pathQueue, (weight + next_weight, newPath))


def BFS(graph, start, end):
    """幅優先探索を行うメソッド"""

    initPath = [start]
    pathQueue = [initPath]
    while len(pathQueue) != 0:
        tmpPath = pathQueue.pop(0)
        print('Current BFS path:', printPath(tmpPath))
        lastNode = tmpPath[-1]
        if lastNode == end:
            return tmpPath
        for (weight, nextNode) in graph.childrenOf(lastNode):
            if nextNode not in tmpPath:
                newPath = tmpPath + [nextNode]
                pathQueue.append(newPath)

def testSP():
    """テストメソッド"""

    nodes = []
    for name in range(9):
        nodes.append(Node(str(name)))
    g = Digraph()
    for n in nodes:
        g.addNode(n)
    g.addEdge(WeightedEdge(nodes[0], nodes[1], 2))
    g.addEdge(WeightedEdge(nodes[0], nodes[2], 3))
    g.addEdge(WeightedEdge(nodes[0], nodes[3], 4))
    g.addEdge(WeightedEdge(nodes[1], nodes[4], 2))
    g.addEdge(WeightedEdge(nodes[1], nodes[5], 4))
    g.addEdge(WeightedEdge(nodes[2], nodes[5], 1))
    g.addEdge(WeightedEdge(nodes[2], nodes[6], 2))
    g.addEdge(WeightedEdge(nodes[2], nodes[7], 3))
    g.addEdge(WeightedEdge(nodes[3], nodes[8], 6))

    sp = BFS(g, nodes[0], nodes[5])
    print('Shortest path found by BFS:', printPath(sp), '\n')

    sp = UCS(g, nodes[0], nodes[5])
    print('Shortest path found by UCS:', printPath(sp))
testSP()

    実行結果は下記のようになります。UCSメソッドでは重みを考慮しているため、最終的なパスは0->2->5になっています。

    Current BFS path: 0
Current BFS path: 0->1
Current BFS path: 0->2
Current BFS path: 0->3
Current BFS path: 0->1->4
Current BFS path: 0->1->5
Shortest path found by BFS: 0->1->5

Current UCS path: 0  weight: 0
Current UCS path: 0->1  weight: 2
Current UCS path: 0->2  weight: 3
Current UCS path: 0->1->4  weight: 4
Current UCS path: 0->3  weight: 4
Current UCS path: 0->2->5  weight: 4
Shortest path found by UCS: 0->2->5

    まとめ

    12章では練習問題をみていきながら優先順位付きキューを用いた重み付き有向グラフの経路探索を実装してみました。 実装においてはWikipediaの均一コスト探索のページや、 Pythonの公式ドキュメントにある優先順位付きキューの説明を参考にさせていただきました。

    in  CS, Algorithm, Python

    計算複雑性の対数はどこからくるのか？

    Pythonプログラミングイントロダクション10章まで読みました。 9,10章は計算複雑性についてです。O(n)となる線形な計算量はイメージしやすいのですが、O(log n) のように対数が出てくるケースがどういうケースか最初イメージしずらかった覚えがあります。

    この本では、9章で計算複雑性についての概念を、10章では二分探索やマージソートを例に、計算複雑性に対数が現れる様子を詳しく説明してくれています。

    計算複雑性

    9章で下記の計算複雑性について説明されています。

    O(1)定数計算時間
    O(log n)対数計算時間
    O(n)線形計算時間
    O(n log n)対数線形計算時間
    O(n^k)多項式計算時間k:定数
    O(c^n)指数計算時間c:定数

    前述したように定数計算時間や線形計算時間はイメージしやすいです。定数計算時間なら入力によらず計算時間は一定となり、線形計算時間なら入力に比例して計算時間が増加します。

    計算複雑性に対数が現れるケース

    本書では O(log n): 対数計算時間や、O(n log n):線形対数計算時間となる場合を二分探索とマージソートを例に説明してくれています。

    対数計算時間と二分探索

    下記は二分探索のコード例です。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

    def binary_search(lis, val):
    u""" 引数で与えられたListの中から検索valの位置を検索して返す。
    検索値が存在しない場合は-1を返す
    """

    length = len(lis)
    if length == 0:
        return -1

    return _search_array(lis, val,  0, length - 1)

def _search_array(lis, val, start, end):

    mid = int((start + end) / 2)
    if start == end  and lis[mid] != val:
        return -1

    if lis[mid] == val:
        return mid

    elif lis[mid] > val:
        if (start == mid):
            return -1
        return _search_array(lis, val, start, mid - 1)

    else:
        return _search_array(lis, val, mid + 1, end)

    return -1

print(binary_search([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12], 1))
print(binary_search([1, 3, 5, 8], 4))

    : 0
: -1

    _search_binaryメソッドは与えられたリストを元に、検索する値が存在しない場合はリストの長さが1になるまで、リストの長さを半分にしながら再帰し続けます。 つまり、再帰回数をxとしたときに、

    \[ 2^x = リストの長さ \]

    \[ x = \log_{2} (リストの長さ) \]

    \[ リストの長さを n とすると \]

    \[ x = \log_{2} n \]

    つまり計算複雑性は O(log n)となります。こうやって対数が計算複雑性に現れます。

    線形対数計算時間とマージソート

    下記はマージソートのコード例です。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

    def merge_sort(lis):
    return split_list(lis)

def split_list(arr):
    """
    リストを半分に分ける
    リストの要素が2つになったところで比較を行い、比較した結果をmerge_arrメソッドに渡す。
    """
    if len(arr) <= 1:
        return arr
    elif len(arr) == 2:
        if arr[0] > arr[1]:
            return [arr[1], arr[0]]
        else:
            return arr

    else:
        br = int(len(arr) / 2)
        return merge_arr(split_list(arr[:br]), split_list(arr[br:]))

def merge_arr(arr1, arr2):
    """
    ソート済みの渡されたリストを相互に比較しながらマージする。
    """

    ret = list()
    len1 = len(arr1)
    len2 = len(arr2)

    i = j = 0
    arr1_val = arr1[i]
    arr2_val = arr2[j]

    while len(ret) < len1 + len2:

        if arr1_val < arr2_val:
            ret.append(arr1_val)
            if i < len1 - 1:
                i += 1
                arr1_val = arr1[i]
            else:
                arr1_val = float('inf')

        elif arr1_val >= arr2_val:
            ret.append(arr2_val)
            if j < len2 - 1:
                j += 1
                arr2_val = arr2[j]
            else:
                arr2_val = float('inf')

    return ret

print(merge_sort([]))
print(merge_sort([1]))
print(merge_sort([1, 10, 2, 3, 5, 4, 0]))

    : []
: [1]
: [0, 1, 2, 3, 4, 5, 10]

    split_listメソッドは与えられたリストの長さを元にすると、リストの長さが2以下になるまで再帰し続けます。これは二分探索と同じ計算時間になりますので、O(log n)になります。 merge_arrメソッドでは、while文でリストの長さ分ループしながら比較して要素の位置を更新していますので、計算時間は O(n)になります。 よって、これら二つを掛け合わせたものが計算時間になるので、O(n lon n)となります。

    まとめ

    9,10章から対数が現れる計算複雑性について取り上げました。対数が現れる計算複雑性のケースを有名なアルゴリズムとセットで学ぶことができました。 10章ではハッシュデータ構造についても言及があり、チェーン法のような実装が提示されていますが、15章で詳しく取り扱うとのこと。読み進める楽しみができました。

    in  CS, Algorithm, Python

    リスコフの置換原則(LSP)をPyhonで考える

    Pythonプログラミングイントロダクション8章まで読み終わりました。

    6,7章はさらっと読み進められましたので飛ばして、今回は8章をみていきます。この章ではオブジェクト指向についての説明がされています。 継承、カプセル化、オーバーライド等のオブジェクト指向やクラスの定番の話題が説明がされている中で、リスコフの置換原則について軽く触れられていましたので詳しくみていきたいと思います。

    リスコフの置換原則

    本書ではリスコフの置換原則についてはさらっと説明されていますが、詳しく見ていきたいと思います。 下記はリスコフの置換原則に関する引用です。

    サブクラスを用いてクラス階層を定義する時、
サブクラスはそのスーパークラスの振る舞いを拡張するように作るべきである.

もしスーパークラスのインスタンスを用いたコードが正しく動作するならば、
それはサブクラスのインスタンスに置き換えても正しく動作するように設計すべきである。

    SuperHogeを継承したSubHogeのインスタンスがFugaServiceで利用されるケースを考えます。 FugaServiceのprocessメソッドではSuperHoge、SubHogeの両方のインスタンスを受け取れますが、どちらが渡ってきても動作します。 動作した結果が意図通りであれば問題ありません。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

    class FugaService:
    def process(self, hoge):
        hoge.echo()


class SuperHoge:
    def echo(self):
        print('super hoge')

class SubHoge(SuperHoge):
    def echo(self):
        print('sub hoge')


service = FugaService()
super_hoge = SuperHoge()
sub_hoge=SubHoge()

service.process(super_hoge)
service.process(sub_hoge)

    : super hoge
: sub hoge

    下記の例は意図通りではない継承のパターンです。 Employeeクラスを継承するEngineerクラスがあり、在職期間を管理しています。 親クラスのEmployeeクラスのperiodメソッドは’年’を引数にとることを前提としていますが、子クラスのEngineerクラスでは’月’を引数にとることを前提としています。 在職期間を元に有給付与とかしているプログラムがあったりるとバグってしまいますね。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

    class Employee:
    year = 0
    month = 0
    def period(self, year):
        self.year = int(year)
        self.month = int((year - int(year)) * 12)


class Engineer(Employee):
    def period(self, month):
        self.year = int(month / 12)
        self.month = int(month % 12)

def print_exist(employee, year):
    employee.period(year)
    print('在職期間は' , employee.year , '年' , employee.month , 'ヶ月です')

employee = Employee()
engineer = Engineer()

print_exist(employee, 1.5)
print_exist(engineer, 1.5)

    : 在職期間は 1 年 6 ヶ月です
: 在職期間は 0 年 1 ヶ月です

    意図通りでないオーバーライドがある場合、インスタンスのタイプによって処理を分けるようなif文を書いたりする必要があります。上記の例だとEmpoyeeだと年を、Engineerだと月を引数に渡すような処理をif文で加えます。

    上記の例の解決策もそうなのですが、そもそもメソッドのオーバーライドをやめさせたい場合もあるかと思います。常に親クラスのメソッドが呼ばれるようにしたい場合です。その場合は単に子クラスでのオーバーライドを止めれば良いです。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

    class FugaService:
    def process(self, hoge):
        hoge.echo()


class SuperHoge:
    def echo(self):
        print('super hoge')

class SubHoge(SuperHoge):
    pass

service = FugaService()
super_hoge = SuperHoge()
sub_hoge=SubHoge()

service.process(super_hoge)
service.process(sub_hoge)

    : super hoge
: super hoge

    オーバーライドをやめるのは簡単ですが、SuperHogeクラスを継承したサブクラスにそもそもオーバーライドさせないようにする方が便利です。 Python3.8以降であれば@finalを利用するのが一つの手です。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

    from typing import final

class FugaService:
    def process(self, hoge):
        hoge.echo()


class SuperHoge:
    @final
    def echo(self) -> None:
        print('super hoge')

class SubHoge(SuperHoge):

    def echo(self) -> None:
        print('sub hoge')

service = FugaService()
super_hoge = SuperHoge()
sub_hoge=SubHoge()

service.process(super_hoge)
service.process(sub_hoge)

    上記のファイルをhoge.pyとして保存して、mypyコマンドで型チェックをすると、下記のようなエラーになります。

    1
2
3

    ❯ mypy hoge.py
hoge.py:15: error: Cannot override final attribute "echo" (previously declared in base class "SuperHoge")
Found 1 error in 1 file (checked 1 source file)

    型チェッカーはPythonランタイムとは別のものなので、開発環境に組み込んだりCIの一環として実装する必要があります。

    まとめ

    8章からリスコフの置換原則について取り上げました。何気に使っているオーバーライドですがリスコフの置換原則を守ることで、無駄なif文がない見通しの良いプログラムになります。

    in  CS, Algorithm, Python

    エイリアシングによるオブジェクトの参照

    Pythonプログラミングイントロダクション5章まで読みました。

    5章をみていきます。この章ではPythonの構造型と呼ばれるtuple ,list, str, rangeについてみていきながら、可変性と不変性の違いが説明されています。 また、関数を引数として渡すような高階関数についても説明されています。

    特にlist型のエイリアシングについて多くの説明がこの章では割かれています。確かにプログラミングでよくミスる部分ではありますね。

    エイリアシング

    下記のように変数aの要素を直接変更したり、変数bに対して副作用のあるappend関数を用いて値を変更すると、cの値も変わってしまいます。

    1
2
3
4
5
6
7
8

    a = [1]
b = [2]
c = [a , b]
print('c : ' , c)

a[0] = 0
b.append(3)
print('c : ' , c)

    >> c :  [[1], [2]]
>> c :  [[0], [2, 3]]

    上記の場合a,b が参照しているリストと、a,b を構成要素として生成されたcが参照しているリストが同一のものになっています。 a,bを通して参照したリストとcを通して参照しているリストは、別の経路から同じリストを参照している状態になっています。

    c = [a[:] , b[:]] のようにスライスを使うと、リストは複製されるため変更してもcの値に影響しません。 a,bが参照しているリストと同じ値のリストを複製しますが、参照しているリストは同じものではなく、全く別のリストを参照している状態になります。

    1
2
3
4
5
6
7
8

    a = [1]
b = [2]
c = [a[:] , b[:]]
print('c : ' , c)

a[0] = 0
b.append(3)
print('c : ' , c)

    >> c :  [[1], [2]]
>> c :  [[1], [2]]

    Pythonではid() 関数により、オブジェクトが同じものを参照しているかを確認することができます。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

    a = [1]
b = a

print(id(a) == id(b))

a.append(2)

print(id(a) == id(b))

b = a[:]

print(id(a) == id(b))

    >> True
>> True
>> False

    要素を直接変更した場合や、append()関数を使った場合はid()関数の戻り値はは変わらないですが、スライスを使うと複製されるためにid()関数の戻り値が変わります。

    まとめ

    5章からエイリアシングについて取り上げました。エイリアシングはわかりにくいバグにつながるケースもあります。なのでimmutableなオブジェクトが好まれることもあります。

    in  CS, Algorithm, Python

    静的スコープと動的スコープの違い

    Pythonプログラミングイントロダクション4章まで読みました。

    この章ではプログラムを書く上で避けては通れない関数、スコープ、抽象化についてです。

    プログラミングにおいては処理をひたすら書いていくだけではなく、共通の処理は関数として切り出したり、変数のスコープを意識して変数が見える範囲を理解する必要があります。 スコープを理解していないと処理の対象がなんなのか、どこまで参照可能なのかを分からずにプログラミングすることになり、効率が悪くなります。

    静的スコープ

    Pythonは静的スコープ(レキシカルスコープ)の言語です。本書で出てくるスコープに関連する用語を整理しておきます。

    名前空間違う名前空間では同じ名前の変数が異なるものとして扱われる。このように分割して衝突を回避する概念
    スコープ変数や関数を参照できる範囲のこと
    局所変数ローカル変数ともいう。関数内で利用できる変数のこと。
    大域変数グローバル変数ともいう。全てのスコープから利用できる変数のこと

    同じ名前の変数 x をプログラム内で使用した場合、それぞれの関数ではどの x が参照されているか見ていきます。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

    def hoge():
    def fuga():
        x = 'fuga'
        print('fuga print x: ' + x)

    def moga():
        print('moga print x: ' + x)


    x = 'hoge'
    print('hoge print x: ' + x)
    fuga()
    moga()
    foo()

def foo():
    print('foo print x: ' + x)


x = 'foo'
hoge()

    出力は下記のようになります。

    : hoge print x: hoge
: fuga print x: fuga
: moga print x: hoge
: foo print x: foo

    下記は全て違うものになります。

    • globalで定義された x
    • hoge関数で定義された x
    • fuga関数で定義された x

    下記は同じものになります。

    • hoge関数で定義された x とmoga関数で参照された x
    • globalで定義された x とfoo関数で参照された x

    このように、関数がどこから呼び出されたかに関係なく、どこに定義されているかで変数のスコープが変わるのが静的スコープになります。 また、Pythonではlocal変数やグローバル変数をlocals()関数やglobals()関数で表示させることができます。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

    def hoge():
    def fuga():
        x = 'fuga'
        print('fuga locals: ', locals())

    def moga():
        print('moga locals: ', locals())


    x = 'hoge'
    fuga()
    moga()
    foo()

    print('hoge locals: ', locals())

def foo():
    print('foo locals: ', locals())

x = 'foo'
hoge()
print('globals: ', globals())

    結果は下記のようになります。同じ変数名 x でfuga, hoge, globalに定義がされていることがわかります。

    : fuga locals:  {'x': 'fuga'}
: moga locals:  {}
: foo locals:  {}
: hoge locals:  {'fuga': <function hoge.<locals>.fuga at 0x1014db440>, 'moga': <function hoge.<locals>.moga at 0x1014db4d0>, 'x': 'hoge'}
: globals:  {'__name__': '__main__', '__doc__': None, '__package__': None, '__loader__': <class '_frozen_importlib.BuiltinImporter'>, '__spec__': None, '__annotations__': {}, '__builtins__': <module 'builtins' (built-in)>, '__file__': '<stdin>', '__cached__': None, 'hoge': <function hoge at 0x1014db320>, 'foo': <function foo at 0x1014db3b0>, 'x': 'foo'}

    動的スコープ

    静的があれば動的もあります。関数がどこから呼び出されたかで変数のスコープが変わるのが動的スコープになります。 bashで変数にlocalをつけると動的スコープになります。

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

    #!/bin/bash
x="hoge"

hoge() {
    echo "in hoge x is $x"
}

foo() {
    local x="foo"
    hoge
}

foo
hoge

    in hoge x is foo
in hoge x is hoge

    foo関数からhoge関数が呼ばれていますが、hoge関数で参照される x はfoo関数が呼び出す直前に設定された x になっています。

    まとめ

    本書で説明されている静的スコープと対比して、動的スコープがどうなっているかを bashのlocal変数の例で整理してみました。 本書ではlocals()関数で表示されるシンボルテーブルの取り扱いをわかりやすい図で説明してくれています。是非こちらも参照してみてください。