CS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import random
from scipy import stats


def get_t_value():
    treatmenDist = (119.5, 5.0)
    controlDist = (120, 4.0)
    sampleSize = 1000

    treatmentTimes, controlTimes = [], []

    for s in range(sampleSize):
        treatmentTimes.append(random.gauss(treatmenDist[0], treatmenDist[1]))
        controlTimes.append(random.gauss(controlDist[0], controlDist[1]))

    controleMeans = sum(controlTimes) / len(controlTimes)
    treatMeans = sum(treatmentTimes) / len(treatmentTimes)

    twoSampleTest = stats.ttest_ind(treatmentTimes, controlTimes, equal_var=False)
    print('Treatmeant mean - control mean = ',
          treatMeans - controleMeans, ' minutes')
    print('The t-statistic from two-sample test is ', twoSampleTest[0])
    print('The p-value from two-sample test is ', twoSampleTest[1])


for i in range(10):
    twoSampleTest = get_t_value()

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

import random
import pylab
import csv

def variance(X):
    """分散"""
    mean = sum(X)/len(X)
    tot = 0.0
    for x in X:
        tot += (x - mean)**2
    return tot/len(X)


def stdDev(X):
    """標準偏差(分散の平方根)"""
    return variance(X)**0.5

def read_anime_score(path):
    """データを読み込みスコアのリストを返す"""
    scores = []
    with open(path, newline='') as f:
        reader = csv.reader(f)
        # skip header
        next(reader)
        for row in reader:
            scores.append(float(row[15]))

    return scores

data = read_anime_score('./anime_cleaned.csv')

# 母平均
popMean = sum(data) / len(data)
# 標本サイズ
sampleSize = 200
numBad = 0
for t in range(10000):
    sample = random.sample(data, sampleSize)
    # 標本平均
    sampleMean = sum(sample) / sampleSize
    # 標準誤差
    se = stdDev(sample) / sampleSize**0.5

    # 母平均と標本平均の誤差から信頼区間外のデータ数を求める
    if abs(popMean - sampleMean) > 1.96 * se:
        numBad += 1
print('Fraction outside 95% confidence interval =', numBad / 10000)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

import pylab
import random


def janken():
    JANKEN_PATTERN = ['G', 'C', 'P']
    while True:
        a_t = random.choice(JANKEN_PATTERN)
        b_t = random.choice(JANKEN_PATTERN)
        if a_t != b_t:
            break
    return janken_judge(a_t, b_t)


def janken_kai():
    JANKEN_WIN_PATTERN = ['G', 'G', 'C', 'P']
    JANKEN_LOSE_PATTERN = ['G', 'C', 'C', 'P']
    while True:
        a_t = random.choice(JANKEN_WIN_PATTERN)
        b_t = random.choice(JANKEN_LOSE_PATTERN)
        if a_t != b_t:
            break
    return janken_judge(a_t, b_t)


def janken_judge(a_t, b_t):
    """ a_tとb_tは違う値の想定。
    aが勝っていたらTrue, 負けていたらFalseを返す """

    win_pattern = [('G', 'C'), ('C', 'P'), ('P', 'G')]
    return (a_t, b_t) in win_pattern


def show_plot(trials, target):
    a_rate = []
    a_win = 0
    for k in range(1, trials + 1):
        if target():
            a_win += 1

        a_rate.append(a_win / k * 100)
    pylab.plot(a_rate)
    pylab.ylim(0, 100)
    pylab.xlim(1, trials)
    pylab.xlabel('times')
    pylab.ylabel('rate')
    pylab.title('Junken')
    pylab.show()


def get_stdDev(trials):
    a_rate = []
    for i in range(0, 100):
        a_win = 0
        for k in range(0, trials):
            if janken():
                a_win += 1
        a_rate.append(a_win / k * 100)
    return stdDev(a_rate)


def variance(X):
    """分散"""
    mean = sum(X)/len(X)
    tot = 0.0
    for x in X:
        tot += (x - mean)**2
    return tot/len(X)


def stdDev(X):
    """標準偏差(分散の平方根)"""
    return variance(X)**0.5


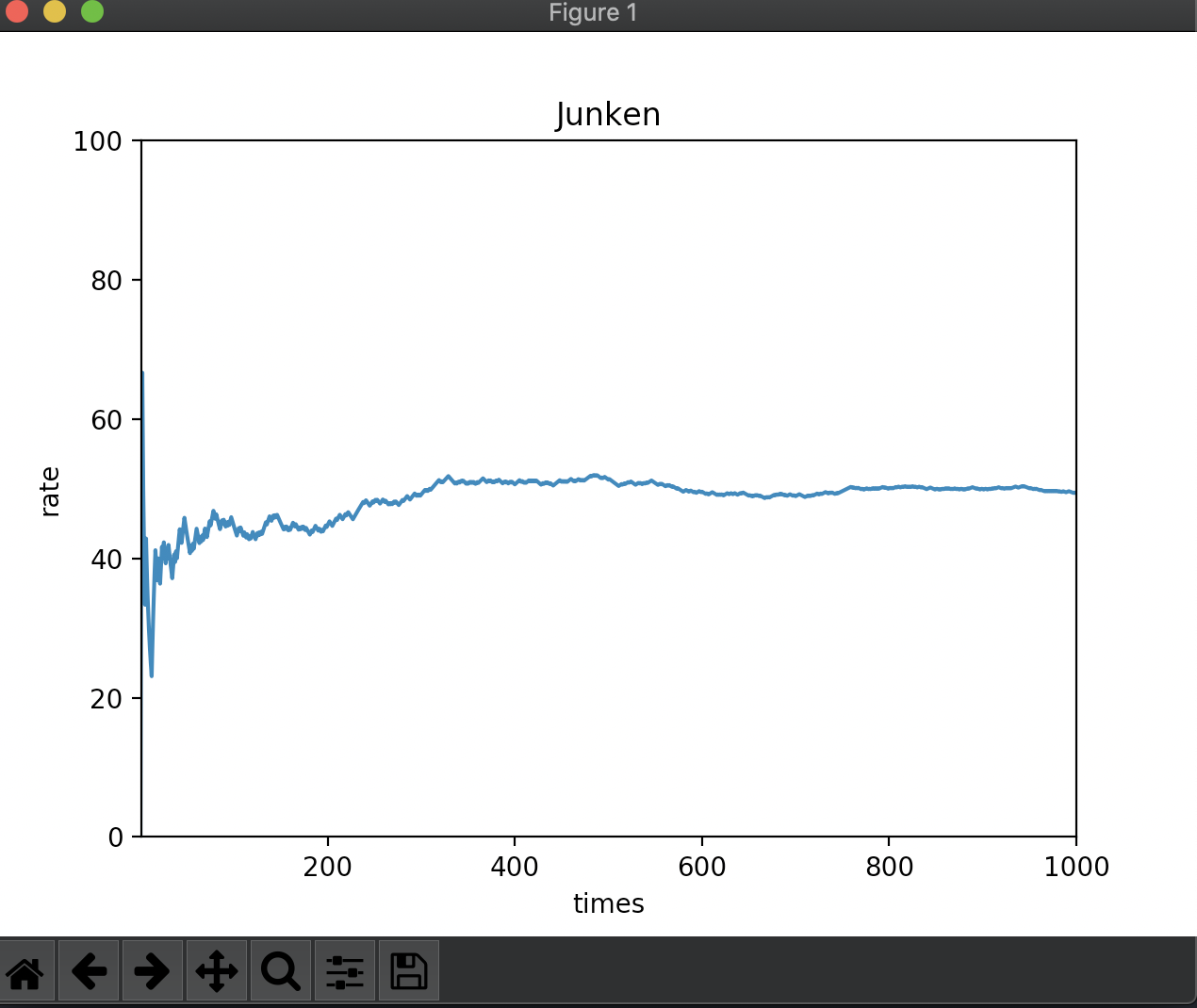
show_plot(1000, janken)
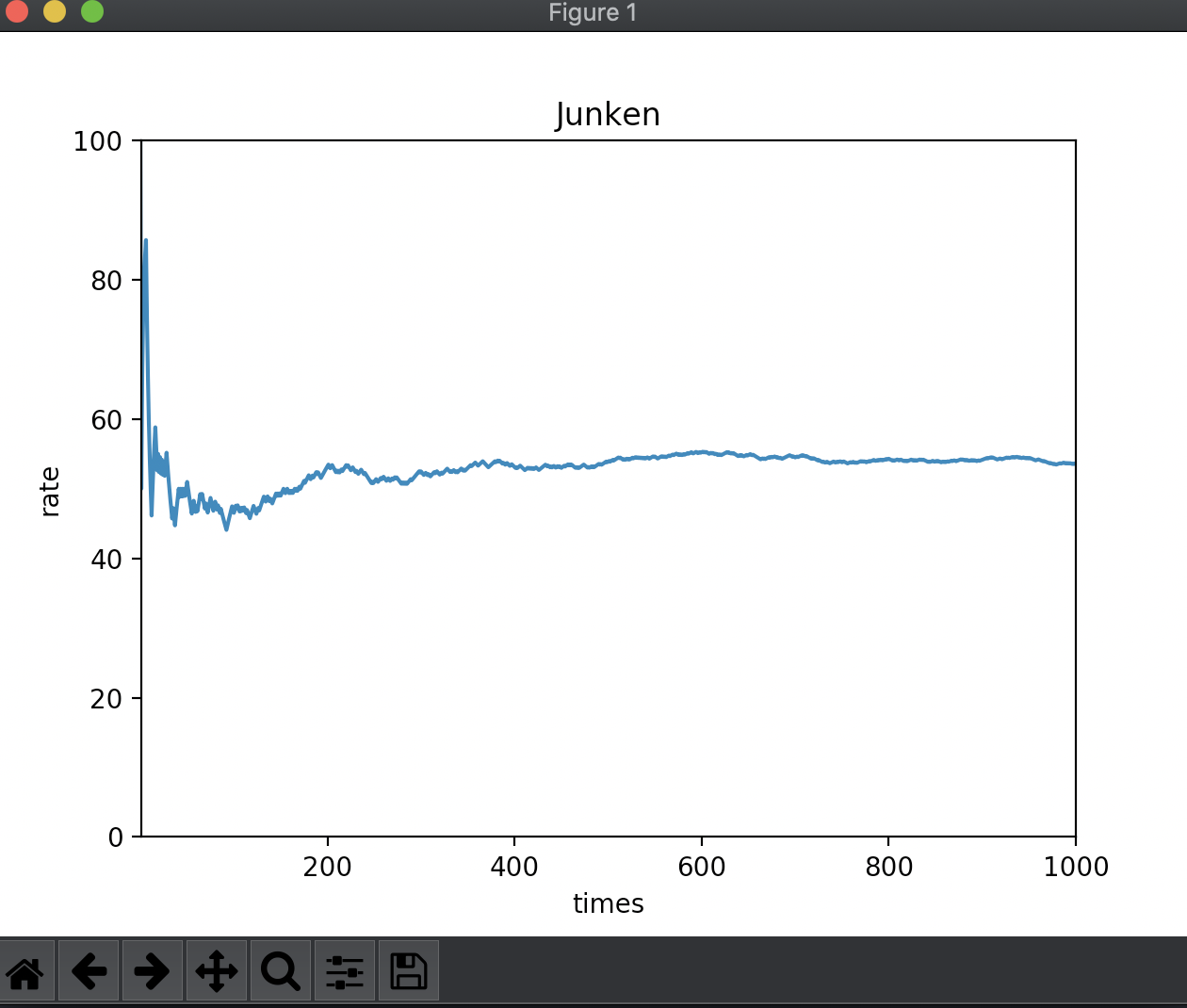
show_plot(1000, janken_kai)
print('10 trials stdDev: ', get_stdDev(10))
print('100 trials stdDev: ', get_stdDev(100))
print('1000 trials stdDev: ', get_stdDev(1000))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import math
import pylab

def binomical_distribution(k, p, t):
    c = math.factorial(k) / (math.factorial(t) * math.factorial(k - t))
    return c * p**t * (1 - p)**(k - t)


def show_plot(p, t):
    x, y = [], []
    for k in range(t, 101):
	x.append(k)
	y.append(binomical_distribution(k, p, t))

    pylab.plot(x)
    pylab.plot(y)
    pylab.ylim(0, 0.5)
    pylab.xlim(2, 100)
    pylab.xlabel('k')
    pylab.ylabel('p')
    pylab.title('Binomical Distribution')
    pylab.show()

show_plot(1 / 6, 2)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Node():

    def __init__(self, node, freq):
        self.freq = freq
        self.node_list = []
        self.node_list.append(node)

    def extend(self, node):
        self.node_list.extend(node.node_list)

    def __lt__(self, other):
        return self.freq < other.freq

def huffman(nodes):
    from heapq import heappush, heappop
    huffmanQueue = []
    ans = {}

    # 優先度つきキューにノードを格納する
    for node in nodes:
        heappush(huffmanQueue, (node.freq, node))

    while len(huffmanQueue) > 1:
        (leftFreq, leftNode) = heappop(huffmanQueue)
        (rightFreq, rightNode) = heappop(huffmanQueue)
        # 一番頻度が少ないノードに'0'を追加
        for s in leftNode.node_list:
            ans[s] = '0' + ans.get(s, '')

        # 二番目に頻度が少ないノードに'1'を追加
        for s in rightNode.node_list:
    	    ans[s] = '1' + ans.get(s, '')

        totalFreq = leftFreq + rightFreq
        leftNode.extend(rightNode)
        heappush(huffmanQueue, (totalFreq, leftNode))
    return ans

print(huffman([Node('a', 5), Node('b', 35), Node('c', 25), Node('d', 15), Node('e', 30)]))

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

class Node(object):
    def __init__(self, name):
        self.name = name

    def getName(self):
        return self.name

    def __str__(self):
        return self.name

    def __lt__(self, i):
        return None


class WeightedEdge(object):
    """重み付きの枝を表すクラス"""

    def __init__(self, src, dest, weight):
        self.src = src
        self.dest = dest
        self.weight = weight

    def getSource(self):
        return self.src

    def getDestination(self):
        return self.dest

    def getWeight(self):
        return self.weight

    def __str__(self):
        return self.src.getName() + '->(' + str(self.weight) + ')' + self.dest.getName()


class Digraph(object):
    """有向グラフを表すクラス"""

    def __init__(self):
        self.nodes = []
        self.edges = {}

    def addNode(self, node):
        if node in self.nodes:
            raise ValueError('Duplicate node')
        else:
            self.nodes.append(node)
            self.edges[node] = []

    def addEdge(self, edge):
        src = edge.getSource()
        dest = edge.getDestination()
        weight = edge.getWeight()
        if not (src in self.nodes and dest in self.nodes):
            raise ValueError('Node not a graph')

        self.edges[src].append((weight, dest))

    def childrenOf(self, node):
        return self.edges[node]

    def __str__(self):
        result = ''
        for src in self.nodes:
            for dest in self.edges[src]:
                result = result + src.getName() + '->' + dest.getName() + '\n'
        return result[:-1]


def printPath(path):
    """パスを表示するメソッド"""
    result = ''
    for i in range(len(path)):
        result = result + str(path[i])
        if i != len(path) - 1:
            result = result + '->'
    return result


def UCS(graph, start, end):
    """重み付き有向グラフを探索するメソッド"""

    initPath = [start]
    pathQueue = []

    from heapq import heappush, heappop
    heappush(pathQueue, (0, initPath))

    while len(pathQueue) != 0:
        (weight, tmpPath) = heappop(pathQueue)

        print('Current UCS path:', printPath(tmpPath), ' weight:', weight)
        lastNode = tmpPath[-1]

        if lastNode == end:
            return tmpPath
        for (next_weight, nextNode) in graph.childrenOf(lastNode):
            if nextNode not in tmpPath:
                newPath = tmpPath + [nextNode]
                heappush(pathQueue, (weight + next_weight, newPath))


def BFS(graph, start, end):
    """幅優先探索を行うメソッド"""

    initPath = [start]
    pathQueue = [initPath]
    while len(pathQueue) != 0:
        tmpPath = pathQueue.pop(0)
        print('Current BFS path:', printPath(tmpPath))
        lastNode = tmpPath[-1]
        if lastNode == end:
            return tmpPath
        for (weight, nextNode) in graph.childrenOf(lastNode):
            if nextNode not in tmpPath:
                newPath = tmpPath + [nextNode]
                pathQueue.append(newPath)

def testSP():
    """テストメソッド"""

    nodes = []
    for name in range(9):
        nodes.append(Node(str(name)))
    g = Digraph()
    for n in nodes:
        g.addNode(n)
    g.addEdge(WeightedEdge(nodes[0], nodes[1], 2))
    g.addEdge(WeightedEdge(nodes[0], nodes[2], 3))
    g.addEdge(WeightedEdge(nodes[0], nodes[3], 4))
    g.addEdge(WeightedEdge(nodes[1], nodes[4], 2))
    g.addEdge(WeightedEdge(nodes[1], nodes[5], 4))
    g.addEdge(WeightedEdge(nodes[2], nodes[5], 1))
    g.addEdge(WeightedEdge(nodes[2], nodes[6], 2))
    g.addEdge(WeightedEdge(nodes[2], nodes[7], 3))
    g.addEdge(WeightedEdge(nodes[3], nodes[8], 6))

    sp = BFS(g, nodes[0], nodes[5])
    print('Shortest path found by BFS:', printPath(sp), '\n')

    sp = UCS(g, nodes[0], nodes[5])
    print('Shortest path found by UCS:', printPath(sp))
testSP()

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

def binary_search(lis, val):
    u""" 引数で与えられたListの中から検索valの位置を検索して返す。
    検索値が存在しない場合は-1を返す
    """

    length = len(lis)
    if length == 0:
        return -1

    return _search_array(lis, val,  0, length - 1)

def _search_array(lis, val, start, end):

    mid = int((start + end) / 2)
    if start == end  and lis[mid] != val:
        return -1

    if lis[mid] == val:
        return mid

    elif lis[mid] > val:
        if (start == mid):
            return -1
        return _search_array(lis, val, start, mid - 1)

    else:
        return _search_array(lis, val, mid + 1, end)

    return -1

print(binary_search([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12], 1))
print(binary_search([1, 3, 5, 8], 4))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

def merge_sort(lis):
    return split_list(lis)

def split_list(arr):
    """
    リストを半分に分ける
    リストの要素が2つになったところで比較を行い、比較した結果をmerge_arrメソッドに渡す。
    """
    if len(arr) <= 1:
        return arr
    elif len(arr) == 2:
        if arr[0] > arr[1]:
            return [arr[1], arr[0]]
        else:
            return arr

    else:
        br = int(len(arr) / 2)
        return merge_arr(split_list(arr[:br]), split_list(arr[br:]))

def merge_arr(arr1, arr2):
    """
    ソート済みの渡されたリストを相互に比較しながらマージする。
    """

    ret = list()
    len1 = len(arr1)
    len2 = len(arr2)

    i = j = 0
    arr1_val = arr1[i]
    arr2_val = arr2[j]

    while len(ret) < len1 + len2:

        if arr1_val < arr2_val:
            ret.append(arr1_val)
            if i < len1 - 1:
                i += 1
                arr1_val = arr1[i]
            else:
                arr1_val = float('inf')

        elif arr1_val >= arr2_val:
            ret.append(arr2_val)
            if j < len2 - 1:
                j += 1
                arr2_val = arr2[j]
            else:
                arr2_val = float('inf')

    return ret

print(merge_sort([]))
print(merge_sort([1]))
print(merge_sort([1, 10, 2, 3, 5, 4, 0]))

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class FugaService:
    def process(self, hoge):
        hoge.echo()


class SuperHoge:
    def echo(self):
        print('super hoge')

class SubHoge(SuperHoge):
    def echo(self):
        print('sub hoge')


service = FugaService()
super_hoge = SuperHoge()
sub_hoge=SubHoge()

service.process(super_hoge)
service.process(sub_hoge)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Employee:
    year = 0
    month = 0
    def period(self, year):
        self.year = int(year)
        self.month = int((year - int(year)) * 12)


class Engineer(Employee):
    def period(self, month):
        self.year = int(month / 12)
        self.month = int(month % 12)

def print_exist(employee, year):
    employee.period(year)
    print('在職期間は' , employee.year , '年' , employee.month , 'ヶ月です')

employee = Employee()
engineer = Engineer()

print_exist(employee, 1.5)
print_exist(engineer, 1.5)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class FugaService:
    def process(self, hoge):
        hoge.echo()


class SuperHoge:
    def echo(self):
        print('super hoge')

class SubHoge(SuperHoge):
    pass

service = FugaService()
super_hoge = SuperHoge()
sub_hoge=SubHoge()

service.process(super_hoge)
service.process(sub_hoge)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

from typing import final

class FugaService:
    def process(self, hoge):
        hoge.echo()


class SuperHoge:
    @final
    def echo(self) -> None:
        print('super hoge')

class SubHoge(SuperHoge):

    def echo(self) -> None:
        print('sub hoge')

service = FugaService()
super_hoge = SuperHoge()
sub_hoge=SubHoge()

service.process(super_hoge)
service.process(sub_hoge)

1
2
3

❯ mypy hoge.py
hoge.py:15: error: Cannot override final attribute "echo" (previously declared in base class "SuperHoge")
Found 1 error in 1 file (checked 1 source file)