Pythonプログラミングイントロダクション(15章)まで読みました。
15章では確率統計を題材に、正規分布や関連する話題として信頼区間について述べられています。
様々な確率統計の題材について、Pythonでの実装とpylabを用いたグラフ表示付きで説明されているので、写経をしていくことで確率統計の知識が深まります。
その中でも確率分布についてみていこうと思います。
様々な確率分布 この章では様々な確率分布を例にPythonでの実装が例示されています。
この章で学ぶ確率分布の一部を列挙してみました。
名称 内容 一様分布 サイコロの目の出る確率のように全ての事象の起こる確率が等しい確率分布 2項分布 成功か失敗のように2つの値しか取らないような場合の確率分布 多項分布 2項分布と異なり、3つ以上の値を取るような場合の確率分布 指数分布 人体の薬物濃度のように指数関数的に濃度が減少していくような場合の確率分布
2項分布の練習問題 上記にあげた確率分布の中でも、2項分布については練習問題がついていたのでみていこうと思います。
練習問題は下記になります。
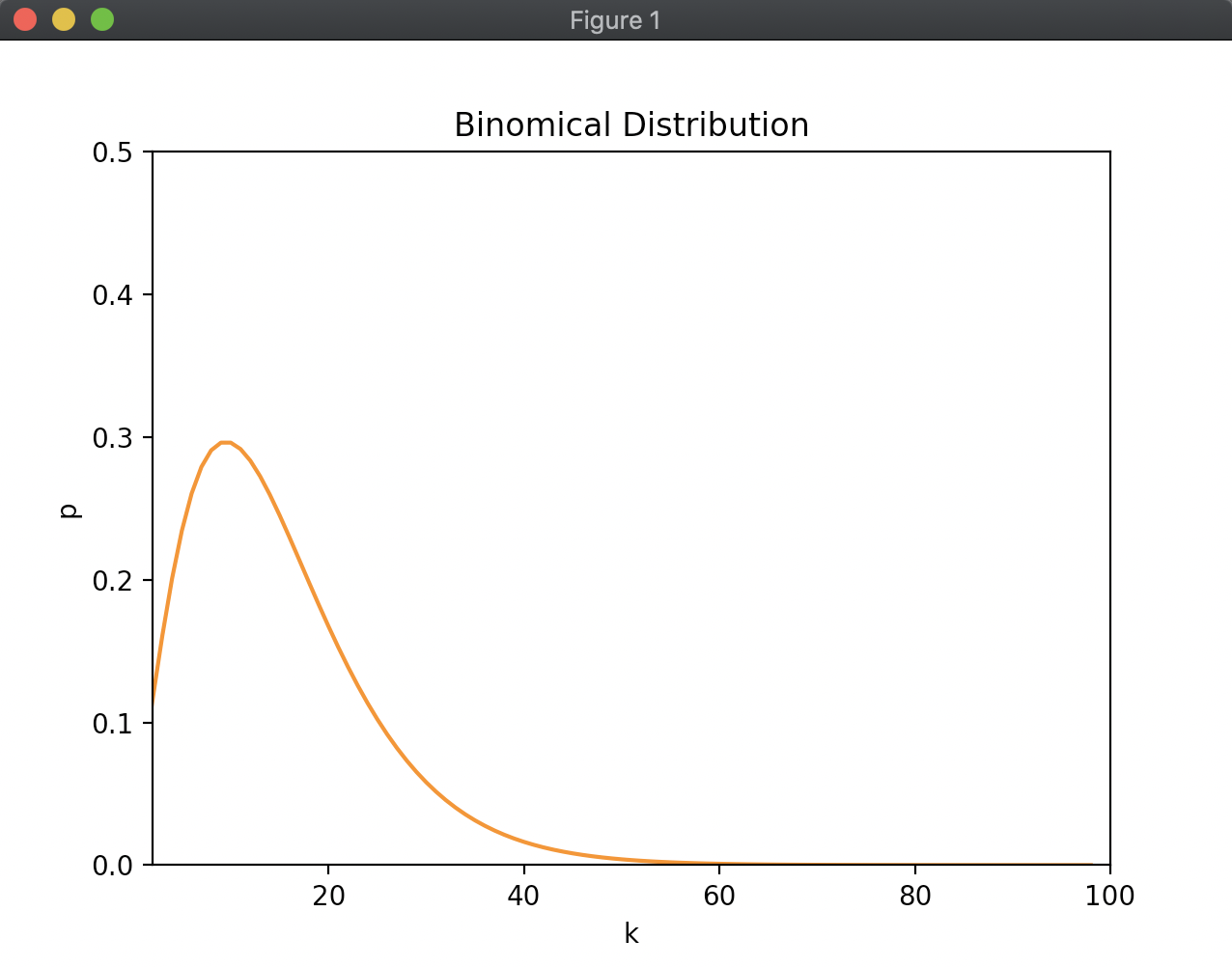
k回の公平なサイコロ投げでちょうど3が2回出る確率を計算する関数を実装せよ。
この関数を用いて、kを2から100まで変化させたときの確率をプロットせよ。
まず、サイコロを投げて3が出る確率は 1/6 になります。
k回サイコロを投げて2回しか3がでず、残りは3以外の数字が出るということになります。
k回サイコロを投げて3が2回出る組み合わせを考える必要があります。
k = 2 のときは
\[ \frac{1}{6} * \frac{1}{6} \]
k = 3 のときは、1,2回目が3の時、1,3回目が3の時、2,3回目が3の時の3通りの確率を足し合わせます。
\[ \frac{1}{6} * \frac{1}{6} * \frac{5}{6} + \frac{1}{6} * \frac{5}{6} * \frac{1}{6} + \frac{5}{6} * \frac{1}{6} * \frac{1}{6}\]
このような2項分布と呼ばれる確率分布の式は以下で表されます。
\[ {}_k \mathrm{ C }_t P^t(1 - P)^{k - t} = \frac { k! } { t!(k - t)! } P^t(1 - P)^{k - t} \]
Pythonでの実装は下記のようになります。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import math
import pylab
def binomical_distribution (k, p, t):
c = math. factorial(k) / (math. factorial(t) * math. factorial(k - t))
return c * p** t * (1 - p)** (k - t)
def show_plot (p, t):
x, y = [], []
for k in range (t, 101 ):
x. append(k)
y. append(binomical_distribution(k, p, t))
pylab. plot(x)
pylab. plot(y)
pylab. ylim(0 , 0.5 )
pylab. xlim(2 , 100 )
pylab. xlabel('k' )
pylab. ylabel('p' )
pylab. title('Binomical Distribution' )
pylab. show()
show_plot(1 / 6 , 2 )
まとめ 2項分布の指練習について、実際にPythonで実装してみました。
この章で学んだ信頼区間についてはこの後でも深掘りされていくようなので楽しみです。
引き続きPythonプログラミングイントロダクション(12章)をみていきます。
この章ではナップザック問題を題材に貪欲アルゴリズムについて説明がされていますが、貪欲アルゴリズムはハフマン符号という符号化にも利用されています。
そして、ハフマン符号はJPEGやZIPで利用されている符号化です。
JPEGやZIPのような馴染みのある要素技術として利用されているハフマン符号とは何か、貪欲アルゴリズムの使いどころはどこなのかをみていきます。
ハフマン符号 ある文章の情報を表現するときにそれぞれの文字に2進数を割り当てたとしたとします。
文章中によく出る文字には短い2進数の割り当てを行い、あまり出てこない文字には長い2進数の割り当てを行うと、全体として短い2進数で文章を表現できるかもしれません。
これがハフマン符号です。
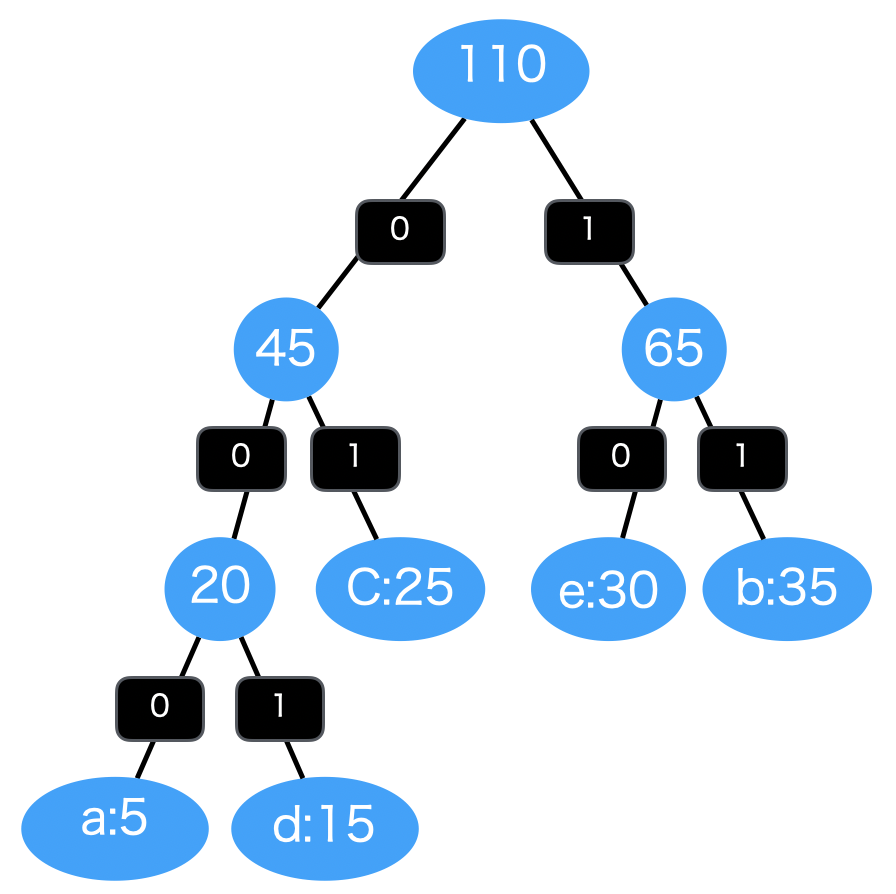
簡単な例として、a,b,c,d,eの文字が文章内に出てくる頻度を表にしました。
頻度の一番多い b には短い2進数 11 が割り当てられ、頻度の一番少ない a には長い2進数 000 が割り当てられています。
文字 頻度 割り当て a 5 000 b 35 11 c 25 01 d 15 001 e 30 10
Pythonによる実装 この割り当てを求めるためのPythonによる実装は下記になります。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Node ():
def __init__(self, node, freq):
self. freq = freq
self. node_list = []
self. node_list. append(node)
def extend (self, node):
self. node_list. extend(node. node_list)
def __lt__(self, other):
return self. freq < other. freq
def huffman (nodes):
from heapq import heappush, heappop
huffmanQueue = []
ans = {}
# 優先度つきキューにノードを格納する
for node in nodes:
heappush(huffmanQueue, (node. freq, node))
while len (huffmanQueue) > 1 :
(leftFreq, leftNode) = heappop(huffmanQueue)
(rightFreq, rightNode) = heappop(huffmanQueue)
# 一番頻度が少ないノードに'0'を追加
for s in leftNode. node_list:
ans[s] = '0' + ans. get(s, '' )
# 二番目に頻度が少ないノードに'1'を追加
for s in rightNode. node_list:
ans[s] = '1' + ans. get(s, '' )
totalFreq = leftFreq + rightFreq
leftNode. extend(rightNode)
heappush(huffmanQueue, (totalFreq, leftNode))
return ans
print (huffman([Node('a' , 5 ), Node('b' , 35 ), Node('c' , 25 ), Node('d' , 15 ), Node('e' , 30 )]))
Nodeクラスは頻度と文字を管理するクラスです。文字はそのノード配下にある全ての文字を管理できるようにリストで配下の文字を管理しています。
まず出現頻度が一番低い文字と二番目に低い文字を探し出します。この時、前回も利用した優先度付きキューを利用して出現頻度が低い順にpopしています。
最終的に割り当てられる二進数文字はディクショナリで管理しています。一番目に出現頻度が低い文字には'0’を、二番目に頻度が少ないノードには'1’を追加していきます。
この2つのノードについて頻度を足し合わせた数を求め、ノードも結合した物を再度優先度付きキューに格納します。
改めてこの優先度付きキューについて出現頻度が低いものから順に同様の処理を行います。このように、頻度が低いノードをひたすら処理していくことで、割り当て文字を求めていきます。
実行結果は下記のようになります。
: {'a': '000', 'd': '001', 'c': '01', 'e': '10', 'b': '11'}
図で表すと下記のようになります。最初に a , d が処理され、 0, 1 が割り振られます。2つの出現頻度を足し合わせた 20 と二つのノードを結合させたものを優先度付きキューに再度格納します。
続いてこの 20 の出現頻度のノード ( a と d が結合したもの ) と c について処理を行います。 a , d には 0 が追加で割り振られ、 c には 1 が割り振られます。あとは同様に頻度を足し合わせ、ノードを結合していきながら繰り返し処理を行なっています。
まとめ 貪欲アルゴリズムを題材にハフマン符号について取り上げました。
そこまで複雑ではないアルゴリズムが、普段利用しているファイル形式の内部で利用されているということでテンションの上がる内容でした。
Pythonプログラミングイントロダクション12章まで読みました。
12章は最適化問題についてです。
空き巣が最適な盗みをはたらくためにはどのようなアルゴリズムで物を選んで盗んでいけば良いかを考えるナップザック問題や、
島をつなぐ橋を丁度一度ずつ渡るような散歩が可能か、オイラーによって定式化されたケーニヒスベルクの橋の問題などのグラフ最適化問題が題材になっています。
最短路問題としては深さ優先探索と幅優先探索が取り上げて、実装について丁寧に説明してくれています。
グラフ最適化問題の仕上げとして、章の最後に重み付き有向グラフの探索アルゴリズムについての練習問題があります。
この練習問題を元に重み付き有向グラフの探索問題を考えていきました。
探索アルゴリズム 練習問題をみていく前に、12章で紹介されている探索アルゴリズムについて軽くみていきます。
幅優先探索 (breadth first search: BFS) まずは探索をスタートするノードに接続する全ての子ノードを探索します。
探索対象がなければ、それぞれの子ノードについて、さらにその子ノードを探索していきます。
まずは同じレベルの子ノードを全て探索してから、次の深さの子ノードを探索していきます。
深さ優先探索 (depth-first search: DFS) 探索した子ノードにさらに子ノードがあった場合は、その子ノードを優先して探索していきます。
とにかく子ノードが見つかったら真っ先にそちらを探索していく形です。
重み付き有向グラフと幅優先探索 そして本章の最後には下記の問題が提示されています。
重み付き有向グラフを考えよう.
幅優先探索アルゴリズムによって最初に見つけられたパスは,
枝の重みの合計が最小であることを保証されているか?
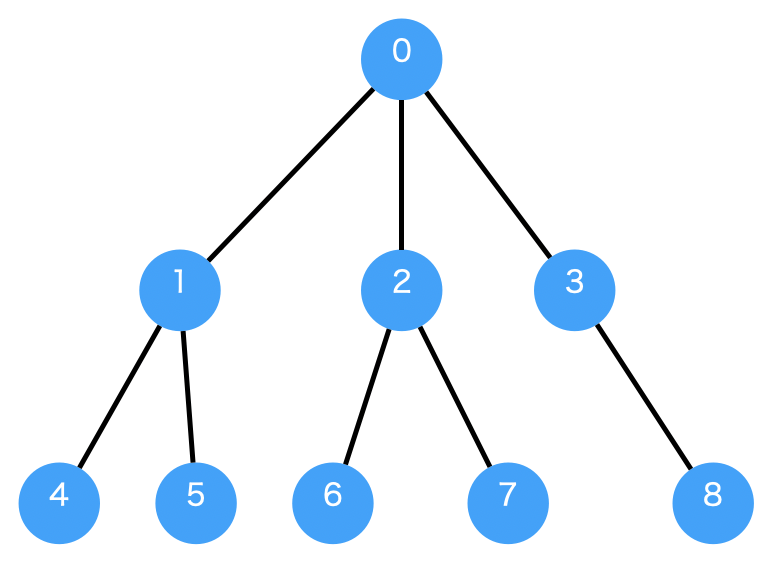
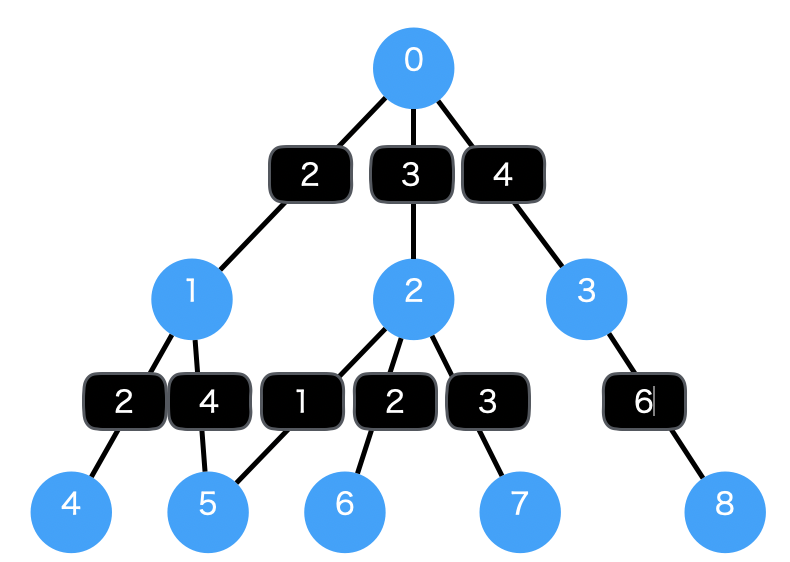
下記の図は重み付きの有向グラフの例です。ノードをつなぐ枝に重みが付いています。この重みを足した数字が幅優先探索で最小になるかというのが練習問題の問いになります。
この例で0からスタートして5を探索する幅優先探索を実施すると0 -> 1 -> 5 (重み6) が導き出されてしまいます。欲しい答えは 0 -> 2 -> 5 (重み4) ですから枝の重みが最小であることは保証されていませんね。
さて、どうすれば良いかというと、優先順位付きキューを用います。この場合、合計した重みが少ないパスを優先的に探索します。
下記は本書のプログラムを一部拝借しつつ、重みを扱えるようにしました。そして重みが一番少ないパスを探索するUCSメソッドを優先順位付きキューを用いて実装しています。
ちょっと長いですが全部載せておきます。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
class Node (object ):
def __init__(self, name):
self. name = name
def getName (self):
return self. name
def __str__(self):
return self. name
def __lt__(self, i):
return None
class WeightedEdge (object ):
"""重み付きの枝を表すクラス"""
def __init__(self, src, dest, weight):
self. src = src
self. dest = dest
self. weight = weight
def getSource (self):
return self. src
def getDestination (self):
return self. dest
def getWeight (self):
return self. weight
def __str__(self):
return self. src. getName() + '->(' + str (self. weight) + ')' + self. dest. getName()
class Digraph (object ):
"""有向グラフを表すクラス"""
def __init__(self):
self. nodes = []
self. edges = {}
def addNode (self, node):
if node in self. nodes:
raise ValueError ('Duplicate node' )
else :
self. nodes. append(node)
self. edges[node] = []
def addEdge (self, edge):
src = edge. getSource()
dest = edge. getDestination()
weight = edge. getWeight()
if not (src in self. nodes and dest in self. nodes):
raise ValueError ('Node not a graph' )
self. edges[src]. append((weight, dest))
def childrenOf (self, node):
return self. edges[node]
def __str__(self):
result = ''
for src in self. nodes:
for dest in self. edges[src]:
result = result + src. getName() + '->' + dest. getName() + ' \n '
return result[:- 1 ]
def printPath (path):
"""パスを表示するメソッド"""
result = ''
for i in range (len (path)):
result = result + str (path[i])
if i != len (path) - 1 :
result = result + '->'
return result
def UCS (graph, start, end):
"""重み付き有向グラフを探索するメソッド"""
initPath = [start]
pathQueue = []
from heapq import heappush, heappop
heappush(pathQueue, (0 , initPath))
while len (pathQueue) != 0 :
(weight, tmpPath) = heappop(pathQueue)
print ('Current UCS path:' , printPath(tmpPath), ' weight:' , weight)
lastNode = tmpPath[- 1 ]
if lastNode == end:
return tmpPath
for (next_weight, nextNode) in graph. childrenOf(lastNode):
if nextNode not in tmpPath:
newPath = tmpPath + [nextNode]
heappush(pathQueue, (weight + next_weight, newPath))
def BFS (graph, start, end):
"""幅優先探索を行うメソッド"""
initPath = [start]
pathQueue = [initPath]
while len (pathQueue) != 0 :
tmpPath = pathQueue. pop(0 )
print ('Current BFS path:' , printPath(tmpPath))
lastNode = tmpPath[- 1 ]
if lastNode == end:
return tmpPath
for (weight, nextNode) in graph. childrenOf(lastNode):
if nextNode not in tmpPath:
newPath = tmpPath + [nextNode]
pathQueue. append(newPath)
def testSP ():
"""テストメソッド"""
nodes = []
for name in range (9 ):
nodes. append(Node(str (name)))
g = Digraph()
for n in nodes:
g. addNode(n)
g. addEdge(WeightedEdge(nodes[0 ], nodes[1 ], 2 ))
g. addEdge(WeightedEdge(nodes[0 ], nodes[2 ], 3 ))
g. addEdge(WeightedEdge(nodes[0 ], nodes[3 ], 4 ))
g. addEdge(WeightedEdge(nodes[1 ], nodes[4 ], 2 ))
g. addEdge(WeightedEdge(nodes[1 ], nodes[5 ], 4 ))
g. addEdge(WeightedEdge(nodes[2 ], nodes[5 ], 1 ))
g. addEdge(WeightedEdge(nodes[2 ], nodes[6 ], 2 ))
g. addEdge(WeightedEdge(nodes[2 ], nodes[7 ], 3 ))
g. addEdge(WeightedEdge(nodes[3 ], nodes[8 ], 6 ))
sp = BFS(g, nodes[0 ], nodes[5 ])
print ('Shortest path found by BFS:' , printPath(sp), ' \n ' )
sp = UCS(g, nodes[0 ], nodes[5 ])
print ('Shortest path found by UCS:' , printPath(sp))
testSP()
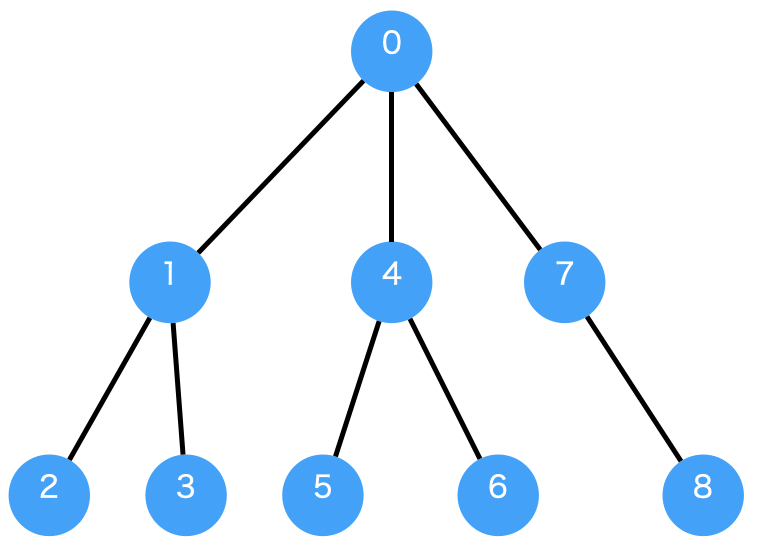
実行結果は下記のようになります。UCSメソッドでは重みを考慮しているため、最終的なパスは0->2->5になっています。
Current BFS path: 0
Current BFS path: 0->1
Current BFS path: 0->2
Current BFS path: 0->3
Current BFS path: 0->1->4
Current BFS path: 0->1->5
Shortest path found by BFS: 0->1->5
Current UCS path: 0 weight: 0
Current UCS path: 0->1 weight: 2
Current UCS path: 0->2 weight: 3
Current UCS path: 0->1->4 weight: 4
Current UCS path: 0->3 weight: 4
Current UCS path: 0->2->5 weight: 4
Shortest path found by UCS: 0->2->5
まとめ 12章では練習問題をみていきながら優先順位付きキューを用いた重み付き有向グラフの経路探索を実装してみました。
実装においてはWikipediaの均一コスト探索のページ や、 Pythonの公式ドキュメントにある優先順位付きキューの説明 を参考にさせていただきました。
Pythonプログラミングイントロダクション10章まで読みました。
9,10章は計算複雑性についてです。O(n)となる線形な計算量はイメージしやすいのですが、O(log n) のように対数が出てくるケースがどういうケースか最初イメージしずらかった覚えがあります。
この本では、9章で計算複雑性についての概念を、10章では二分探索やマージソートを例に、計算複雑性に対数が現れる様子を詳しく説明してくれています。
計算複雑性 9章で下記の計算複雑性について説明されています。
O(1) 定数計算時間 O(log n) 対数計算時間 O(n) 線形計算時間 O(n log n) 対数線形計算時間 O(n^k) 多項式計算時間 k:定数 O(c^n) 指数計算時間 c:定数
前述したように定数計算時間や線形計算時間はイメージしやすいです。定数計算時間なら入力によらず計算時間は一定となり、線形計算時間なら入力に比例して計算時間が増加します。
計算複雑性に対数が現れるケース 本書では O(log n): 対数計算時間や、O(n log n):線形対数計算時間となる場合を二分探索とマージソートを例に説明してくれています。
対数計算時間と二分探索 下記は二分探索のコード例です。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def binary_search (lis, val):
u """ 引数で与えられたListの中から検索valの位置を検索して返す。
検索値が存在しない場合は-1を返す
"""
length = len (lis)
if length == 0 :
return - 1
return _search_array(lis, val, 0 , length - 1 )
def _search_array (lis, val, start, end):
mid = int ((start + end) / 2 )
if start == end and lis[mid] != val:
return - 1
if lis[mid] == val:
return mid
elif lis[mid] > val:
if (start == mid):
return - 1
return _search_array(lis, val, start, mid - 1 )
else :
return _search_array(lis, val, mid + 1 , end)
return - 1
print (binary_search([1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 ], 1 ))
print (binary_search([1 , 3 , 5 , 8 ], 4 ))
: 0
: -1
_search_binaryメソッドは与えられたリストを元に、検索する値が存在しない場合はリストの長さが1になるまで、リストの長さを半分にしながら再帰し続けます。
つまり、再帰回数をxとしたときに、
\[ 2^x = リストの長さ \]
\[ x = \log_{2} (リストの長さ) \]
\[ リストの長さを n とすると \]
\[ x = \log_{2} n \]
つまり計算複雑性は O(log n)となります。こうやって対数が計算複雑性に現れます。
線形対数計算時間とマージソート 下記はマージソートのコード例です。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
def merge_sort (lis):
return split_list(lis)
def split_list (arr):
"""
リストを半分に分ける
リストの要素が2つになったところで比較を行い、比較した結果をmerge_arrメソッドに渡す。
"""
if len (arr) <= 1 :
return arr
elif len (arr) == 2 :
if arr[0 ] > arr[1 ]:
return [arr[1 ], arr[0 ]]
else :
return arr
else :
br = int (len (arr) / 2 )
return merge_arr(split_list(arr[:br]), split_list(arr[br:]))
def merge_arr (arr1, arr2):
"""
ソート済みの渡されたリストを相互に比較しながらマージする。
"""
ret = list ()
len1 = len (arr1)
len2 = len (arr2)
i = j = 0
arr1_val = arr1[i]
arr2_val = arr2[j]
while len (ret) < len1 + len2:
if arr1_val < arr2_val:
ret. append(arr1_val)
if i < len1 - 1 :
i += 1
arr1_val = arr1[i]
else :
arr1_val = float ('inf' )
elif arr1_val >= arr2_val:
ret. append(arr2_val)
if j < len2 - 1 :
j += 1
arr2_val = arr2[j]
else :
arr2_val = float ('inf' )
return ret
print (merge_sort([]))
print (merge_sort([1 ]))
print (merge_sort([1 , 10 , 2 , 3 , 5 , 4 , 0 ]))
: []
: [1]
: [0, 1, 2, 3, 4, 5, 10]
split_listメソッドは与えられたリストの長さを元にすると、リストの長さが2以下になるまで再帰し続けます。これは二分探索と同じ計算時間になりますので、O(log n)になります。
merge_arrメソッドでは、while文でリストの長さ分ループしながら比較して要素の位置を更新していますので、計算時間は O(n)になります。
よって、これら二つを掛け合わせたものが計算時間になるので、O(n lon n)となります。
まとめ 9,10章から対数が現れる計算複雑性について取り上げました。対数が現れる計算複雑性のケースを有名なアルゴリズムとセットで学ぶことができました。
10章ではハッシュデータ構造についても言及があり、チェーン法のような実装が提示されていますが、15章で詳しく取り扱うとのこと。読み進める楽しみができました。
Pythonプログラミングイントロダクション8章まで読み終わりました。
6,7章はさらっと読み進められましたので飛ばして、今回は8章をみていきます。この章ではオブジェクト指向についての説明がされています。
継承、カプセル化、オーバーライド等のオブジェクト指向やクラスの定番の話題が説明がされている中で、リスコフの置換原則について軽く触れられていましたので詳しくみていきたいと思います。
リスコフの置換原則 本書ではリスコフの置換原則についてはさらっと説明されていますが、詳しく見ていきたいと思います。
下記はリスコフの置換原則に関する引用です。
サブクラスを用いてクラス階層を定義する時、
サブクラスはそのスーパークラスの振る舞いを拡張するように作るべきである.
もしスーパークラスのインスタンスを用いたコードが正しく動作するならば、
それはサブクラスのインスタンスに置き換えても正しく動作するように設計すべきである。
SuperHogeを継承したSubHogeのインスタンスがFugaServiceで利用されるケースを考えます。
FugaServiceのprocessメソッドではSuperHoge、SubHogeの両方のインスタンスを受け取れますが、どちらが渡ってきても動作します。
動作した結果が意図通りであれば問題ありません。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class FugaService :
def process (self, hoge):
hoge. echo()
class SuperHoge :
def echo (self):
print ('super hoge' )
class SubHoge (SuperHoge):
def echo (self):
print ('sub hoge' )
service = FugaService()
super_hoge = SuperHoge()
sub_hoge= SubHoge()
service. process(super_hoge)
service. process(sub_hoge)
: super hoge
: sub hoge
下記の例は意図通りではない継承のパターンです。
Employeeクラスを継承するEngineerクラスがあり、在職期間を管理しています。
親クラスのEmployeeクラスのperiodメソッドは’年’を引数にとることを前提としていますが、子クラスのEngineerクラスでは’月’を引数にとることを前提としています。
在職期間を元に有給付与とかしているプログラムがあったりるとバグってしまいますね。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Employee :
year = 0
month = 0
def period (self, year):
self. year = int (year)
self. month = int ((year - int (year)) * 12 )
class Engineer (Employee):
def period (self, month):
self. year = int (month / 12 )
self. month = int (month % 12 )
def print_exist (employee, year):
employee. period(year)
print ('在職期間は' , employee. year , '年' , employee. month , 'ヶ月です' )
employee = Employee()
engineer = Engineer()
print_exist(employee, 1.5 )
print_exist(engineer, 1.5 )
: 在職期間は 1 年 6 ヶ月です
: 在職期間は 0 年 1 ヶ月です
意図通りでないオーバーライドがある場合、インスタンスのタイプによって処理を分けるようなif文を書いたりする必要があります。上記の例だとEmpoyeeだと年を、Engineerだと月を引数に渡すような処理をif文で加えます。
上記の例の解決策もそうなのですが、そもそもメソッドのオーバーライドをやめさせたい場合もあるかと思います。常に親クラスのメソッドが呼ばれるようにしたい場合です。その場合は単に子クラスでのオーバーライドを止めれば良いです。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class FugaService :
def process (self, hoge):
hoge. echo()
class SuperHoge :
def echo (self):
print ('super hoge' )
class SubHoge (SuperHoge):
pass
service = FugaService()
super_hoge = SuperHoge()
sub_hoge= SubHoge()
service. process(super_hoge)
service. process(sub_hoge)
: super hoge
: super hoge
オーバーライドをやめるのは簡単ですが、SuperHogeクラスを継承したサブクラスにそもそもオーバーライドさせないようにする方が便利です。
Python3.8以降であれば@finalを利用するのが一つの手です。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from typing import final
class FugaService :
def process (self, hoge):
hoge. echo()
class SuperHoge :
@final
def echo (self) -> None :
print ('super hoge' )
class SubHoge (SuperHoge):
def echo (self) -> None :
print ('sub hoge' )
service = FugaService()
super_hoge = SuperHoge()
sub_hoge= SubHoge()
service. process(super_hoge)
service. process(sub_hoge)
上記のファイルをhoge.pyとして保存して、mypyコマンドで型チェックをすると、下記のようなエラーになります。
1
2
3
❯ mypy hoge.py
hoge.py:15: error: Cannot override final attribute "echo" ( previously declared in base class "SuperHoge" )
Found 1 error in 1 file ( checked 1 source file)
型チェッカーはPythonランタイムとは別のものなので、開発環境に組み込んだりCIの一環として実装する必要があります。
まとめ 8章からリスコフの置換原則について取り上げました。何気に使っているオーバーライドですがリスコフの置換原則を守ることで、無駄なif文がない見通しの良いプログラムになります。